用来探索因果关系。
# 序
使用线性回归、广义线性回归探索环境对个体的影响可能还停留在表面,类似于结构方程模型的复杂模型或许可以更好地探索它们之间的关系。
结构方程模型 是基于变量的协方差矩阵来分析变量之间关系的一种统计方法。通过该方法既可以探讨因变量受哪几个自变量的影响,也可以探讨一个自变量通过什么途径影响因变量,以及探讨在不同情形下自变量对因变量的影响有何不同。该模型是 路径分析 和 测量关系 之和。
下表给出了各种分析方式的解释:
- 回归分析:多个自变量对一个因变量的影响。
- 路径分析:多个自变量对多个因变量的影响。
- 结构方程模型:路径分析+测量关系
- 探索性因子分析(EFA):测量关系(非经典量表,比如自己设计的表)。
- 验证性因子分析(CFA):测量关系(经典量表,比如大佬设计的表)。
# 术语
结构方程模型涵盖以下变量类型:
- 观测变量:又称潜在变量的显性变量 manifest variable /测量指标/指标变量,是量表或问卷等测量工具所得的数据(路径图中以长方形表示,潜在变量的箭头指向观测变量)。
- 潜在变量:又称无法测量的变量/构面 constructs ,是观察变量间所形成的特质或抽象概念,此特质或抽象概念无法直接测量,而要由观察变量测得的数据资料来反映,比如焦虑、态度等。潜在变量包括外生/自变量、内生/因变量、中介变量(路径图中以椭圆形表示)。
- 外生(潜在)变量:指在模型中未受任何其他变量的影响,而直接影响其他变量的变量,只发挥解释变量的作用。外生变量在路径分析图中相当于自变量(自变量;路径图中会指向任何一个其他变量,但不受任何变量以单箭头指涉的变量。表现为没有被箭头指向)。
- 内生(潜在)变量:指在模型中会受到任一变量影响的变量。内生变量在路径分析图中相当于因变量,也就是路径分析图中箭头所指的对象(因变量;路径图会受到任何一个其他变量以单箭头指涉的变量。表现为被箭头指向的潜在变量)。
- 中介变量:当内生变量同时做因变量和自变量时,表示该变量不仅被其他变量影响,还可能对其他变量产生影响。
- 残差变量:指内生潜在变量无法被模型中的外生潜在变量解释的变异量,即结构方程模型中的随机变异部分(用圆形表示,被单向箭头指向的观测变量或潜在变量都应加上残差变量)。
该模型由两部分组成:
- 测量模型:由潜在变量 latent variable 和观测变量 observed variable 组成。就是潜变量和它的观测变量那一坨。
- 结构模型:是潜在变量间因果关系模型的说明。作为“因”的潜在变量称为外因潜在变量 ζ ;作为“果”的潜在变量称为内因潜在变量 η 。
注:整体模型适配度≈每个测量模型适配度的平均(验证性因子分析 CFA 的平均)。
# SEM在期刊论文中的要点
# 构建理论模型
# 提出研究假设
# 描述变量操作定义
# 样本数据收集
# 信度与效度检验
# 模型适配度检验
# 模型调整与修正
# 路径系数分析
# 检验假设与分析
在实际写作中,囿于篇幅限制,可以仅在正文中描述重要部分。
# 构建理论模型
在引言中阐释清概念和概念之间的关系。若结构模型如下图所示,那么引言应该详细阐述社区环境、日常情绪、社交欲望与感知健康的定义,并且通过综述的方式进行评述:
社区环境->日常情绪与社交欲望
日常情绪->社交欲望
社交欲望->感知健康
这几者之间的关系。(概念图,请勿参考

# 提出研究假设
构建好理论模型之后,基于该模型的路径提出研究假设、研究问题,如下图所示。

# 描述变量操作定义
这一部分描述上文中的潜在变量如何测量,即,描述潜在变量的观测变量。如果使用大佬的经典量表,则最好引用大佬的文献,并进行验证性因子分析 CFA 。自己的量表需要进行探索性因子分析 EFA 。最好采用文字+表格的形式描述变量操作定义,如下图所示。

# 样本数据收集
结构方程模型对样本数量有一定要求,具体而言:
不得低于100:5个及以下构面,每个构面需至少含有3个以上观测变量,且公因子方差 communality >0.6。
不得低于150:6-7个构面,适中的公因子方差>0.5。并且没有underidentified构面。
不得低于300:7个及以下构面,公因子方差<0.45,并且有三个及以下underidentified构面。
不得低于500:很多构面。一些构面有较低的公因子方差,或观测变量少于3个。
# 信度与效度检验
信度:即可靠性,它指的是采取同样的方法对同一对象重复进行测量时,其所得结果相一致的程度。从另一方面来说,信度就是指测量数据的可靠程度。系统误差对信度没什么影响,因为系统误差总是以相同的方式影响测量值的,因此不会造成不一致性。反之,随机误差可能导致不一致性,从而降低信度。
信度分析:是对样本数据的内部一致性进行检验。使用Cronbach α系数进行信度检验。如果低于0.6,则认为数据内部一致性不足;达到0.7-0.8时说明量表具有相当的信度。达到0.8-0.9时说明量表信度非常好。一般来说大于0.6就行。
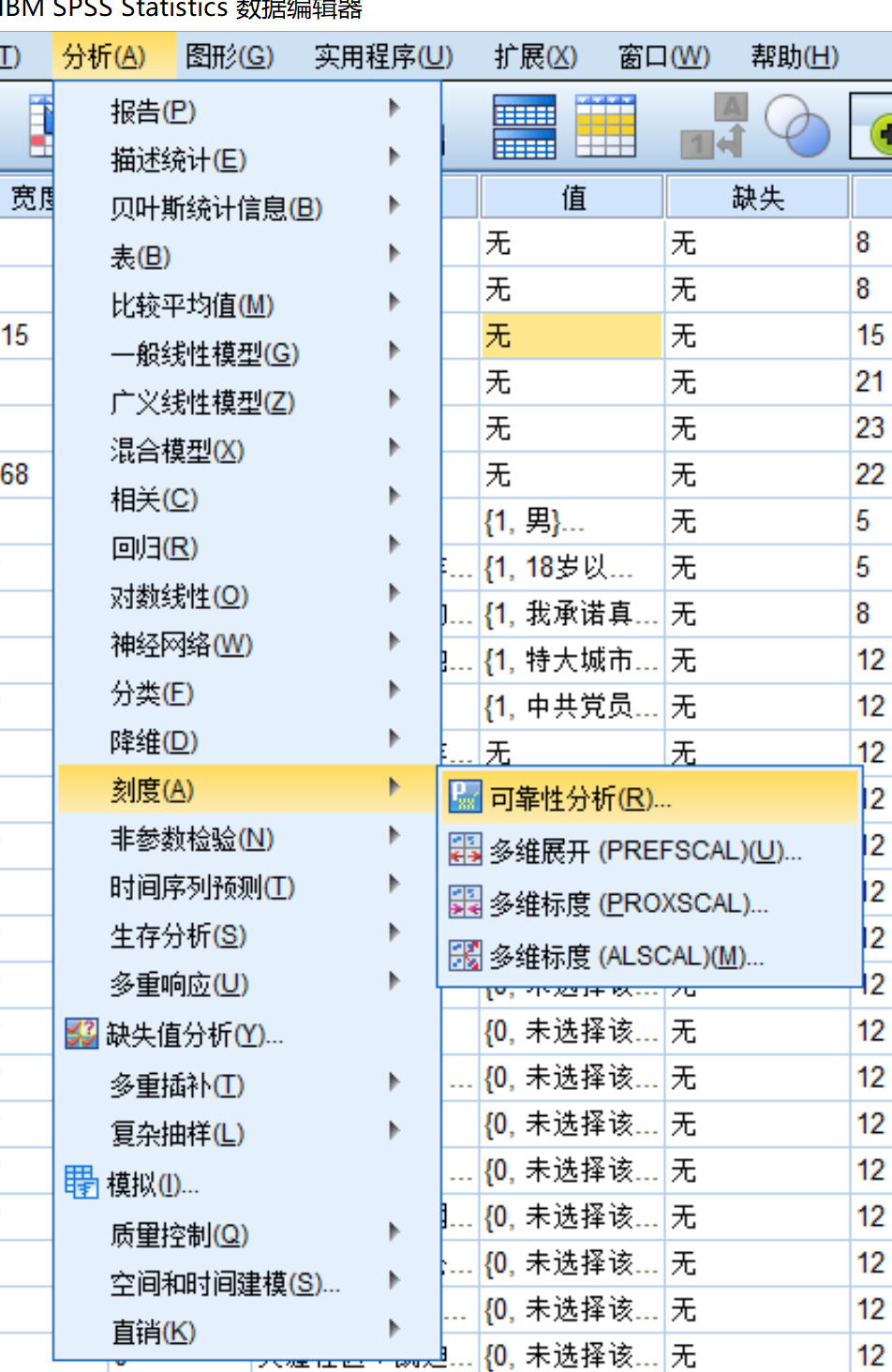
在SPSS中进行信度检验
对每一个构面的观测变量都应进行一次信度检验,如在上图的结构模型中有“社区环境”、“日常情绪”等四个构面,首先对“社区环境”构面的几个观测变量进行一次可靠性检验,得到该构面的 Cronbach’s alpha 系数,若该系数小于0.6,则勾选删除项后的标度。观察每一项的总计相关性,将小于0.3的项删除以提升信度系数。
注:如果是被双向箭头指向的两个潜在变量,需要将他们的观测变量都放进一个可靠性分析。
效度:即有效性。指测量工具或手段能够准确测出所需测量的事物的程度。效度是指所测量到的结果反映所想要考察内容的程度,测到的结果是原本想要测的,测量结果与要考察的内容越吻合,则效度越高;反之,则效度越低。
效度是测量的有效性程度,即测量工具能准确测出其所要测量特质的程度,或简单地说是指一个测验的准确性、有用性。效度是科学的测量工具所必备的重要条件。通过了效度检验才能进行路径分析等后续研究。得到公认有效的问卷设计可以只做验证性因子分析,或省略效度检验步骤。自己设计的表最好都做。
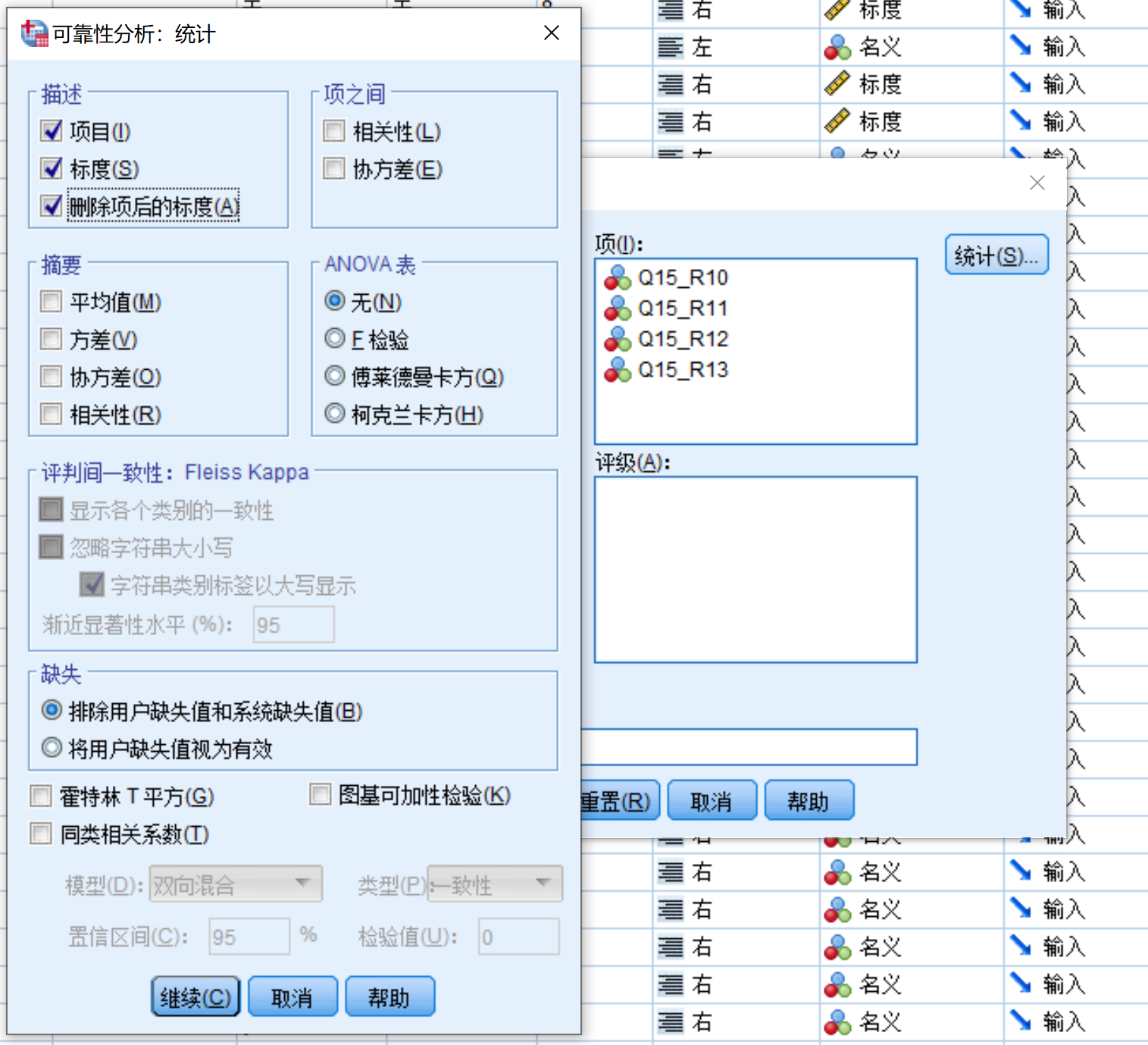
效度分析:在SPSS中,进行因子分析,勾选KMO与Bartlett球形检验。当KMO检验系数>0.5且Bartlett球形检验统计值的显著性(P-value)低于0.05时,做的因子分析才有效。否则说明数据质量低下,不适合做因子分析。
做EFA(使用SPSS)或CFA(使用Amos),前者本质是降维处理,后者包括结构效度、组合效度/收敛效度、区别效度/区分效度。根据Hair, et al (2009)及Fornell and Larcker (1981)的标准:
- 因素负荷量>0.5
- 组成信度 composite reliability, CR >0.6
- 平均变异数萃取量 Average of variance extracted, AVE >0.5或0.36
- 多元相关系数的平方>0.5
探索性因子分析
是一项用来找出多元观测变量的本质结构,并进行降维处理的技术。将所有将要纳入分析的观测变量丢进因子分析里,看能分成几类,哪些观测变量(题目)能聚在一起。注意,这里是检验模型的科学性,不是重新划结构。
以下是分析要点汇总:
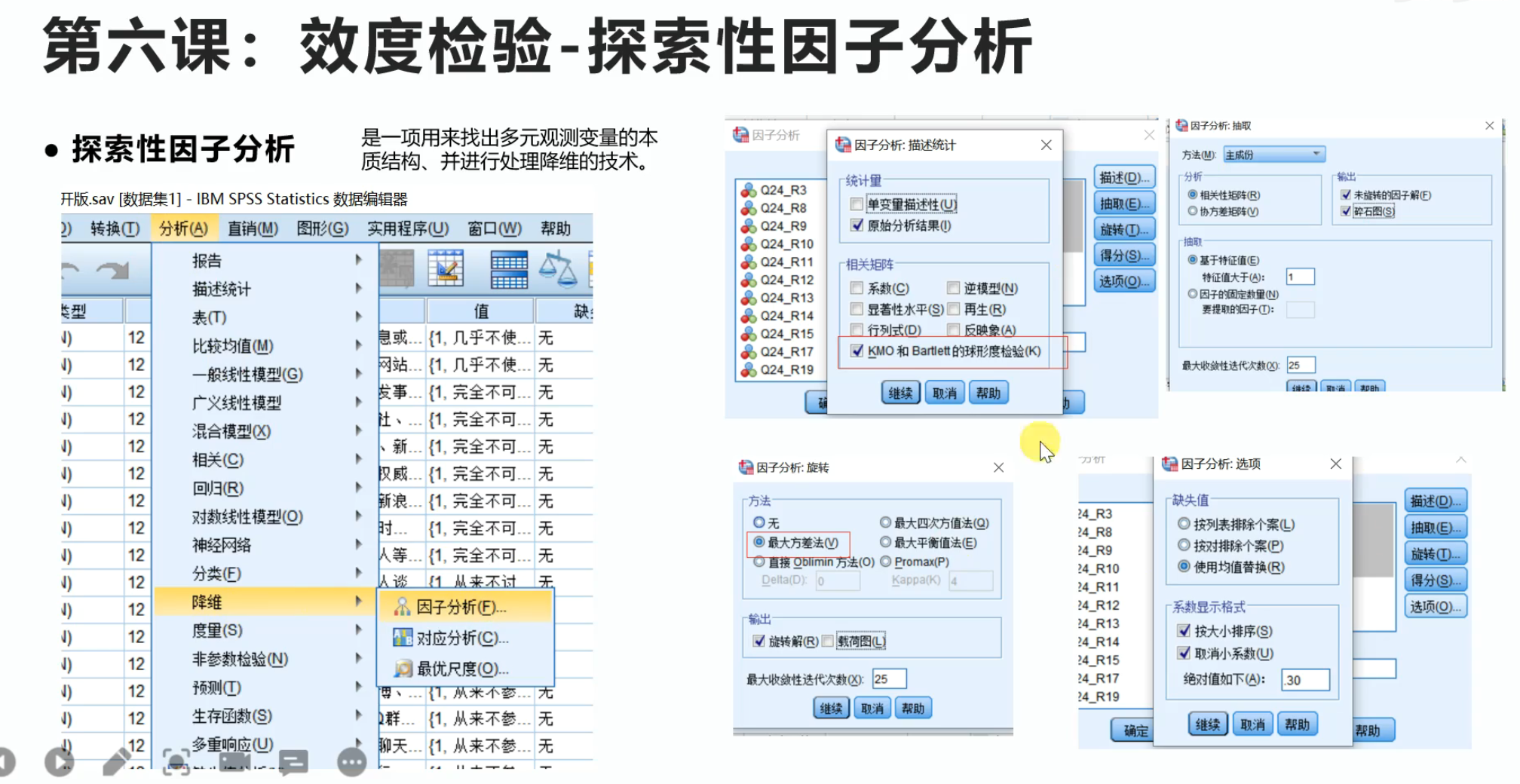
1.查看KMO和Bartlett检验的显著性
需要勾选“KMO和Bartlett的球形度检验”,见上图。
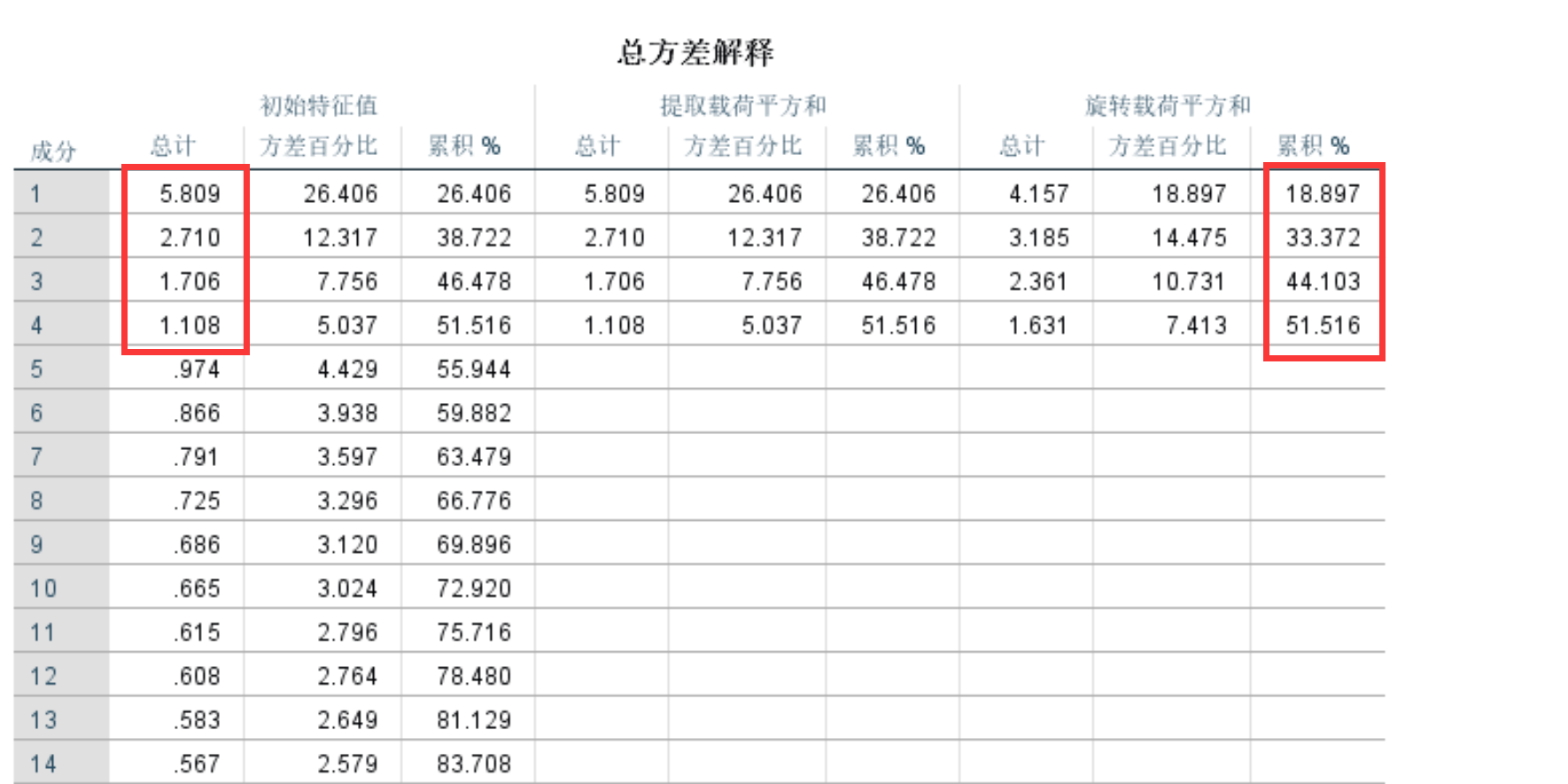
2.解释总方差
查看有多少个载荷值(系数)>1的主成分,这些主成分的旋转平方和载入累计比需要大于60%,最好大于70%。
3.查看碎石图(可选)
查看下降趋势变得平缓的拐点。在解释总方差里找到提炼出的成分的载荷值(系数),有多少个载荷值>1的主成分,拐点就在那个值附近。
4.观察旋转成分矩阵
可以看到上一步提取出的几个主成分中分别包含哪些观测变量。若观测变量的载荷系数大于0.4,或0.5就可以认为该变量属于该主成分。符号影响方向,看绝对值。
根据主成分内的观测变量给构面取名。
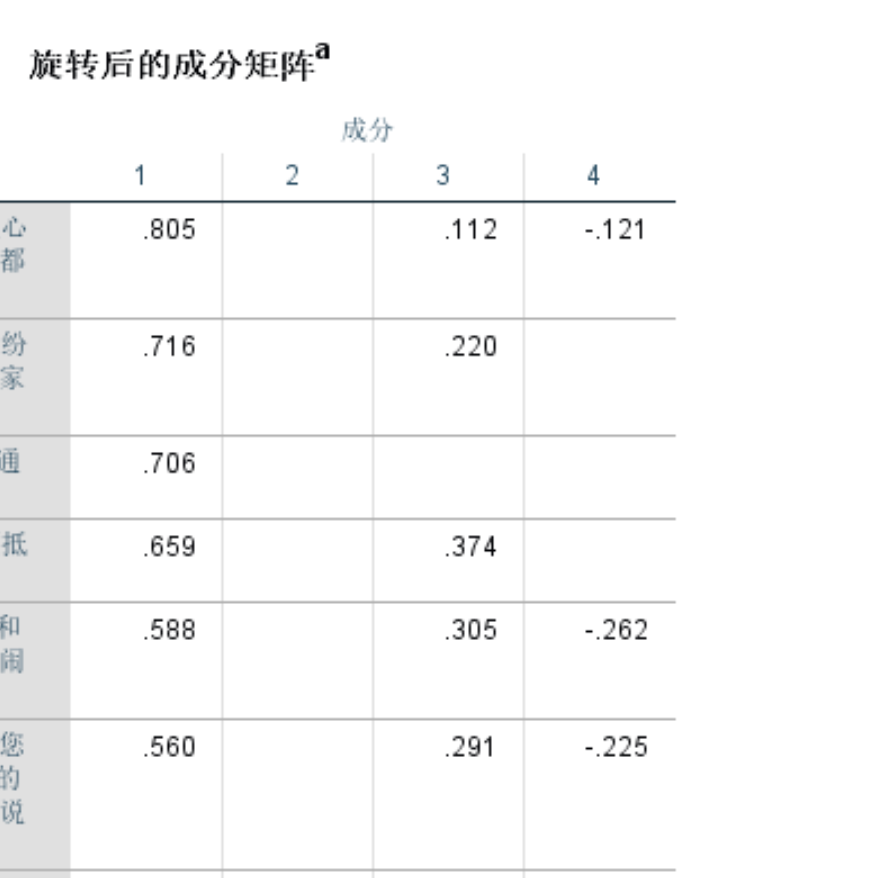
5.论文示例
第一步,给出KMO和Bartlett检验的结果;第二步,解释因子负荷矩阵与方差贡献率是否符合标准。第三步,给出解释,说明把相关的观测变量聚类成多少个主成分,每个主成分包括哪些题目,并对每个主成分进行命名,然后抽象成对应的研究概念。这样就完成了探索性因子分析。
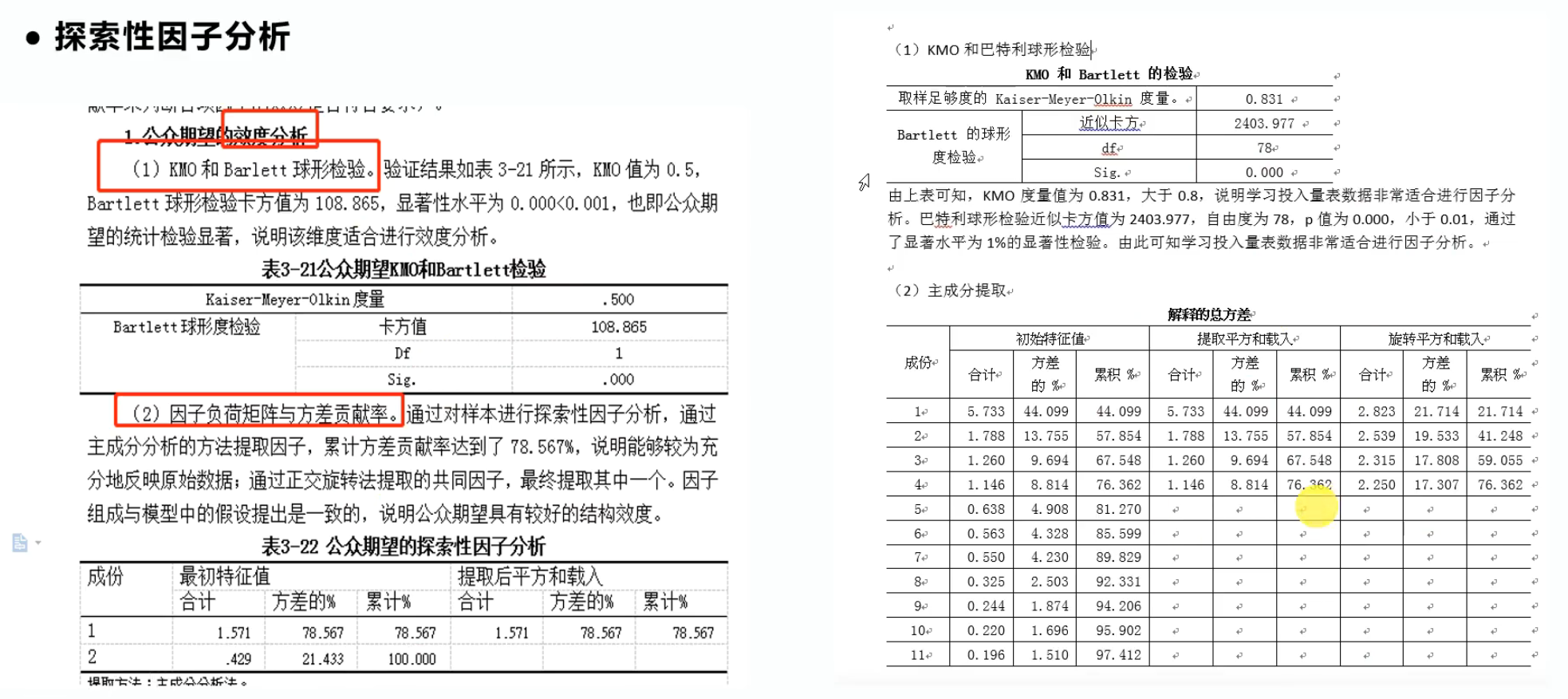
6.排错
若累计方差贡献率、解释性水平不达标,则需要考虑删除题目、删除样本、调整问卷、更替样本。
删除哪些题目?
根据因子分析中的相关性矩阵(在抽取选项卡里选中才会在结果中显示),剔除处于同一构面但是相关性程度低的题目。
在SPSS中进行探索性因子分析
将结构方程模型中所有的观测变量都拖进因子分析,在描述选项卡中勾选KMO和Bartlett检验;在抽取选项卡中勾选碎石图;在旋转选项卡中勾选最大方差法与载荷图;在选项选项卡中勾选按大小排序和取消小系数。
结果中的成分矩阵可以忽略,需要关注的是旋转后的成分矩阵。
详见该图。
若因子分析效果不佳,可以在统计选项卡内勾选系数、显著性水平、行列式,把同一构面低相关性的观测变量删除。
验证性因子分析
通过验证性因子分析可以得到结构效度、组合效度/收敛效度、区别效度/区分效度。其中结构效度见下文。
组合效度:维度内题目的相关性。某个潜变量内题目的一致性是否比其他潜变量的题目的一致性更强。
区别效度:维度间题目的相关性存在,但也存在一定区别性。不同潜变量的题目是否有较强的差异性。
收敛效度
有组合效度 Composite Reliability, CR 和平均变异数萃取量 Average of variance extracted 两种指标来评价。前者用于评估构面内部的一致性,类似于Cronbach’s alpha;后者指潜在变量对观察变量解释能力的平均。
- CR越高表示构面内部一致性越高,越收敛。最好>0.7
- AVE越高,潜变量对观察变量的解释能力越强,收敛效度越高。需要>0.36
这两个指标的计算公式与步骤见向老师视频。
区分效度
与收敛效度是对应的概念,区分效度看的是构面与构面之间的差异性。需要将某个构面的AVE开平方的值与该构面与其他构面的相关系数相比。确保 sqrt(AVE) 最大。每个构面的AVE在收敛效度检验中得到。

# 模型适配度(结构效度)检验
在此之前,一定要确保完成了信度检验和探索性因子分析,筛掉无法通过检验的变量。
在AMOS中拟合结构方程模型后,得到模型的一系列指标(在View Text -> Model Fit选项卡),将这些指标与下表比较,每一项都需要尽量满足要求,才说明模型有效。但这个要求并不绝对,差一点也是可以的。
注:在拟合模型之前,潜在变量与它的观测变量的路径,必须有一条的系数为1。否则无法正常拟合模型。
模型指标:
绝对指标:反应样本共变异系数被模型共变异系数矩阵解释的比例,类似R方
- 卡方 Ⲭ2 :越小越好
- 拟合优度指数 GFI, Goodness of Fit Index :>0.8
- 修正拟合优度指数 AGFI, Adjusted Goodness of Fit Index :>0.9
- 残差均方根 RMR, Root Mean Square Residual :<0.05
- 近似误差均方根 RMSEA, Root Mean Square Error of Approximation :<0.08
相对指标:研究模型的适配度与统计基本模型(虚无模型)相比的改善程度
- 规范拟合指数 NFI, Normed Fit Index :>0.8
- 非规范拟合指数 TLI或NNFI, Tucker-Lewis Index或Non-Normed Fit Index :>0.9
- 增值拟合指数 IFI, Incremental Fit Index :>0.9
- 比较拟合指数 CFI, Comparative Fit Index :>0.9
信息指标:用于竞争模型、比较几个模型)
- 赤池信息准则 AIC, Akaike Information Criterion :越小越好
- 交叉验证指数 ECVI, Expected Cross Validation Index :越小越好
其他指标
- 卡方除以自由度Ⲭ2/df:<3
- SRMR:<0.05
- BIC:越小越好
- NCP:竞争模型,比较几个模型,越小越好。
- HOELTER:在Default栏,95%置信水平下(.05)>200表示样本充足。若<75则表示样本量严重匮乏。
- Parsimony->Adjusted Measures的PNFI和PCFI:>0.5表示模型不太复杂。
论文中必须汇报的三个指标: Ⲭ2/df 、 RMSEA 、 GFI 。此外, IFI 、 TLI 、 CFI 也是论文中的常见指标。
可以通过以下方式进行汇报:
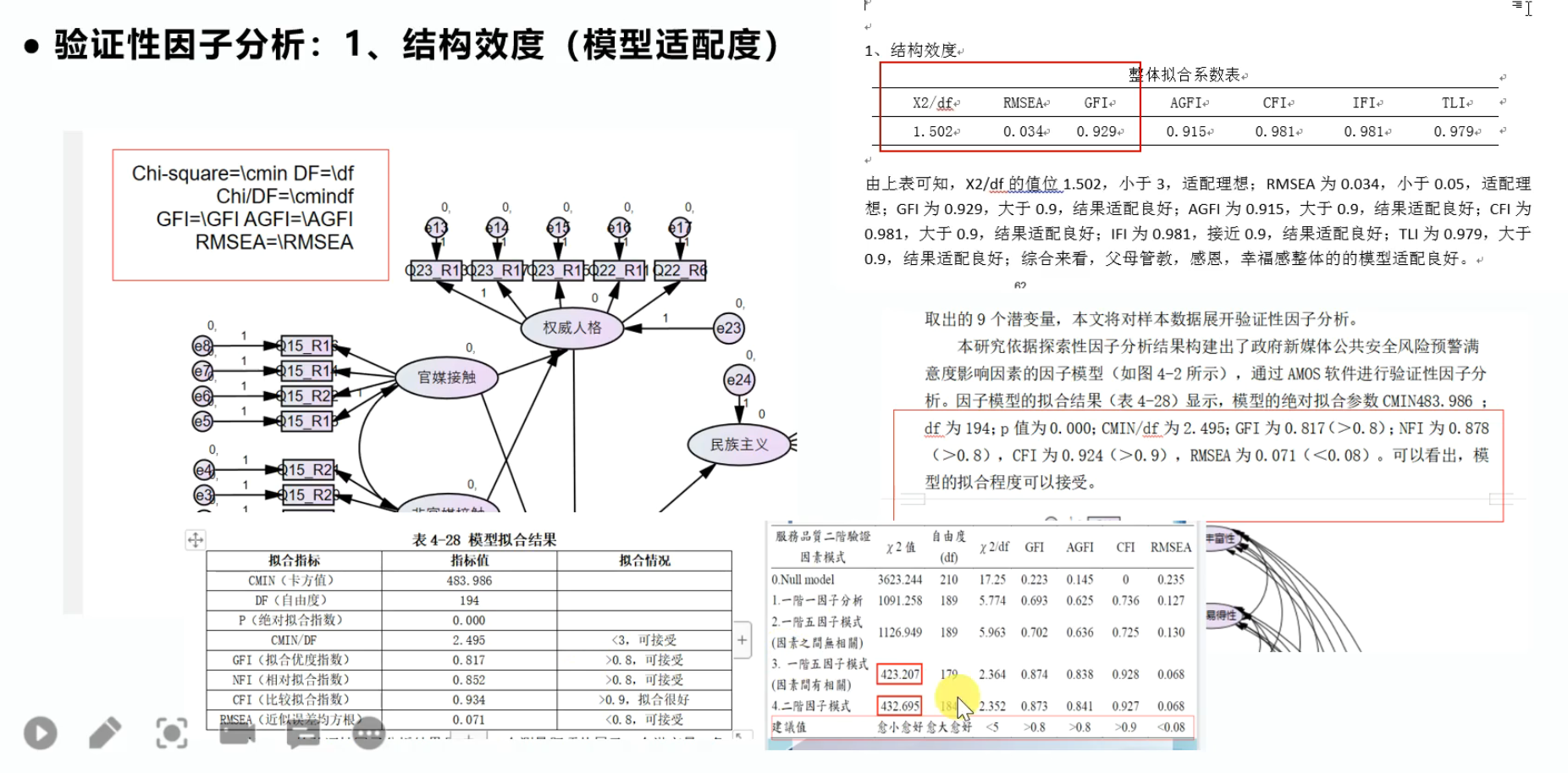
各指标
SEM是基于协方差矩阵分析变量之间关系,它的基本假设是:样本共变异数矩阵=模型共变异数矩阵。
反映模型相似度的指标:GFI、CFI、TLI…(越高越好),最好>0.9(至少>0.5,否则模型太差不存在修正的必要,>0.8可接受)
反映模型差异性的指标:RMSEA、SRMR…(越低越好),最好<0.05(至少<0.5,否则模型太差不存在修正的必要,<0.08可接受)
这些0.9, 0.8, 0.05, 0.08都不是绝对的界限,可以灵活把握,根据研究领域向更宽松浮动。
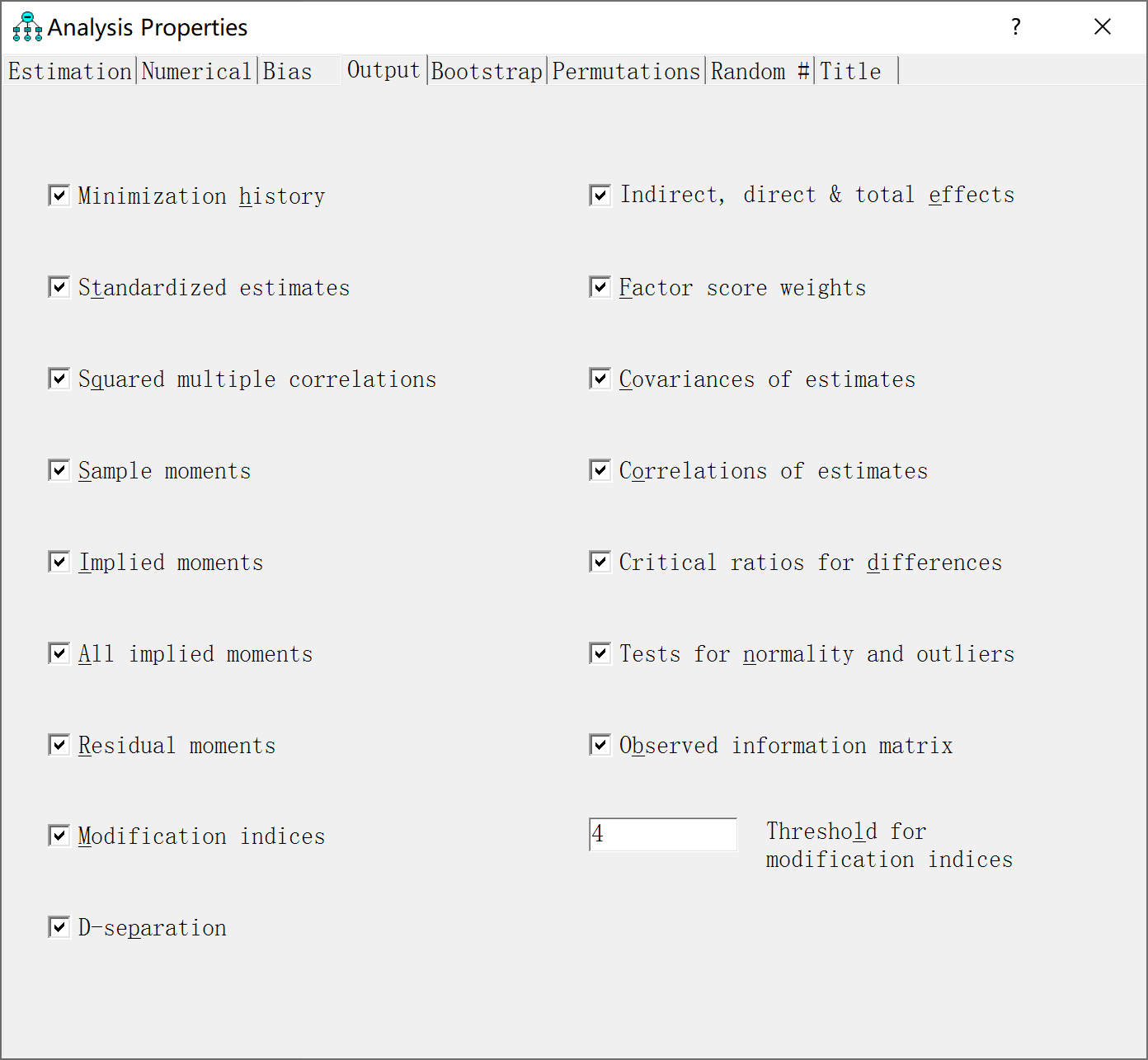
确保结构正确,并且每个潜变量与观测变量有且仅有一条的回归权重为1之后。点击算盘旁边的按钮进行分析属性设置。需要在Output选项卡中勾选全部可选项。按照下图设置。

然后点击算盘按钮进行模型拟合,拟合完成后发现下图中的要素。
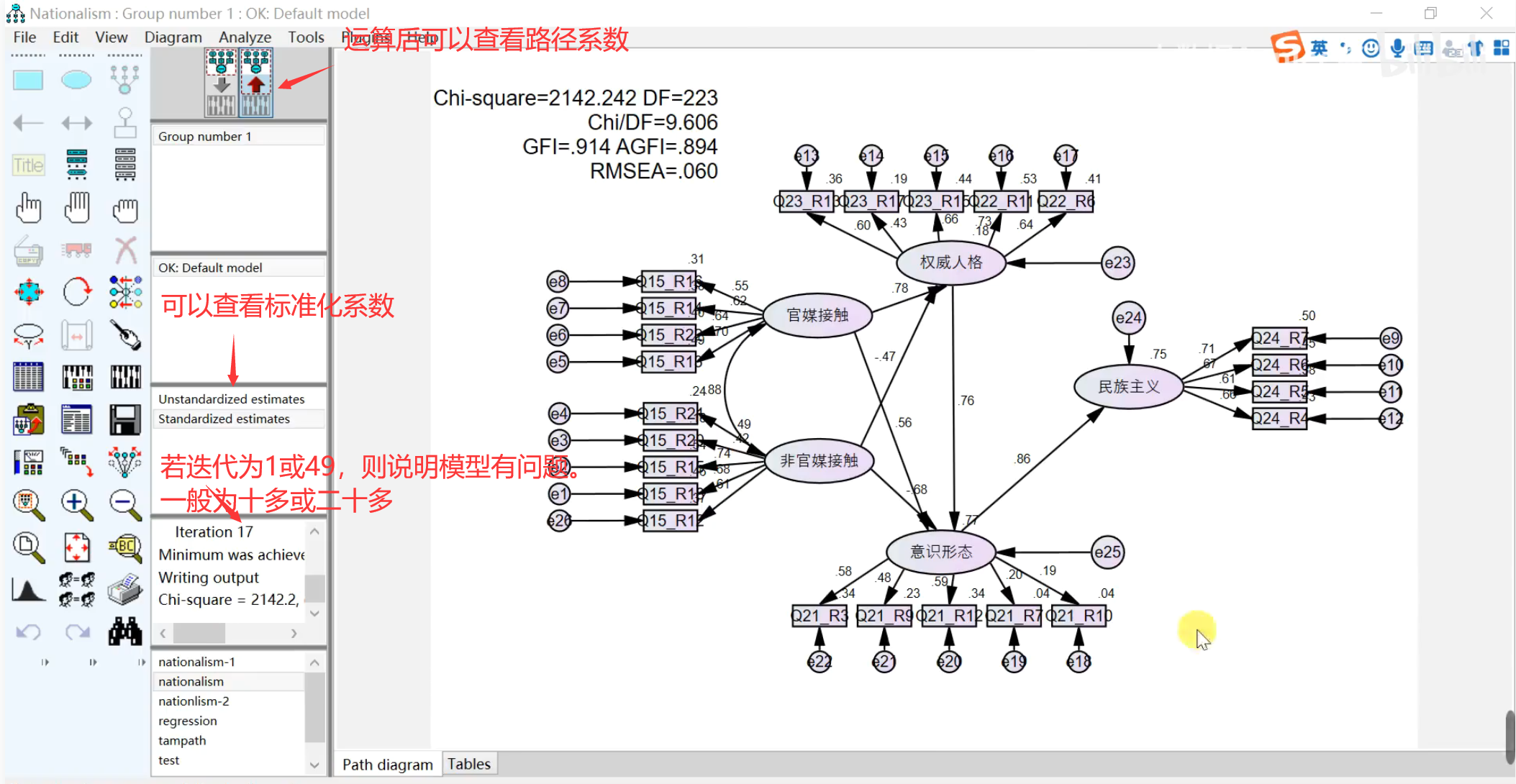
注:图中标准化的路径系数在不同元素之间具有不同含义。潜在变量到观测变量之间的路径系数可以理解为因子载荷量,若模型适配不佳,且因子载荷量<0.6(验证性实验)或0.5(探索性实验),则可以考虑删除该观测变量;残差变量到观测变量路径上的系数称为SMC,实际上是题目的信度,约等于因子载荷量的平方,需要大于0.6;潜在变量之间路径系数指的是影响系数。
# 模型调整与修正
首先通过信效度检验,然后开始模型拟合。
由于整体模型适配度≈每个测量模型适配度平均( CFA 的平均)。所以要对每个测量模型进行修正,以使得整体模型达标。
如果在信效度检验时已删去部分题目、调整了问卷,但整体模型适配度还是不理想,那么参考以下操作:
调整测量模型
1.检查因子载荷量。根据拟合结果的路径系数(因子载荷量)删除题目,从而提升整体模型适配度
参考此处。
如果严格完成信效度检验,实际上不会出现这种可能。因为在分析过程中已经把质量差的题目想剔除了。
2.残差拉相关。
不推荐,因为理论而言,各观测变量的残差应该是独立的。然而残差拉相关之后模型适配度会得到提升。部分期刊论文会使用这种方法。
若要采用这种方法,可参考下图。MI指若将这两个残差变量拉相关,则卡方值会降低多少;Par Change指路径系数会怎么变化。
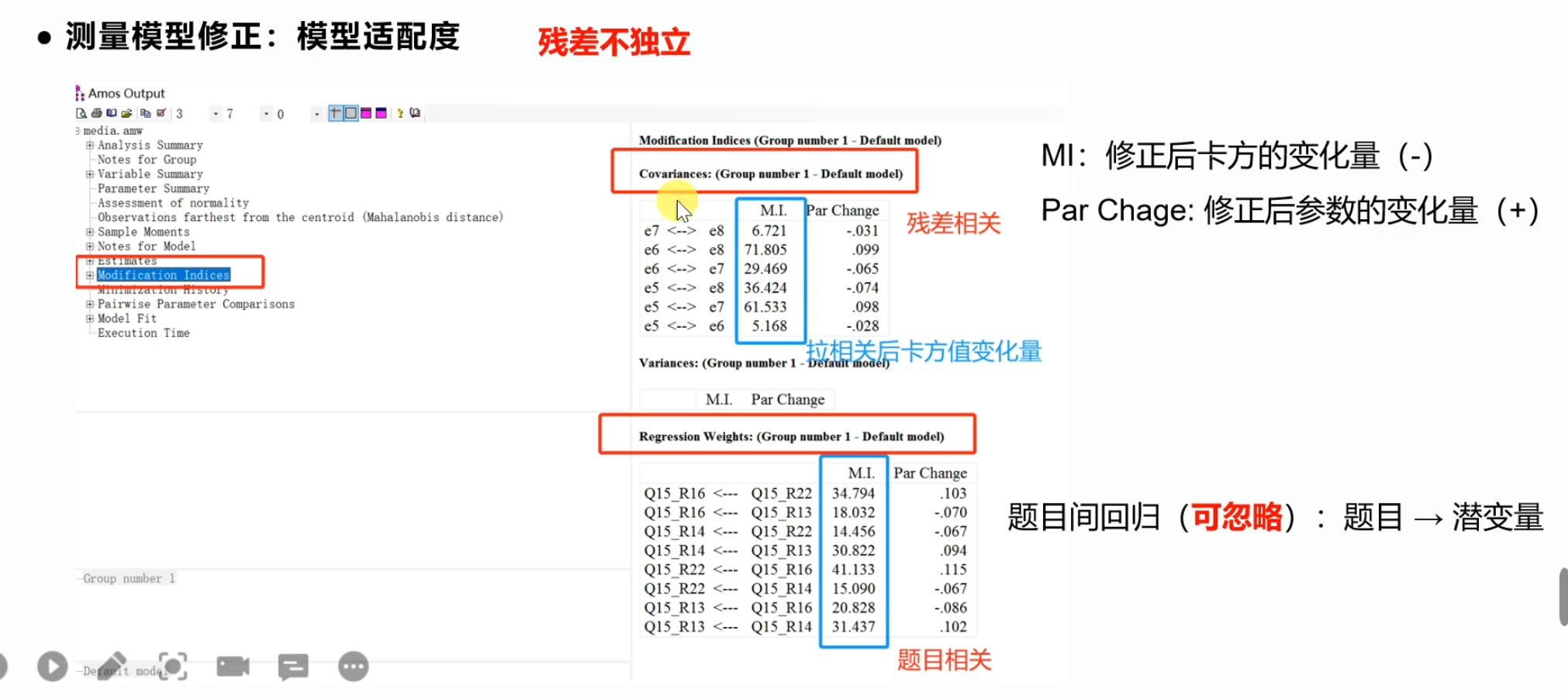
既然拉相关是不推荐的,还有一种方法可以减少卡方值,即删除拉相关后卡方值之和最大的观测变量(下图中红色e8的之和与蓝色的e6之和相比)。此外,如果剔除后观察变量只有3个,那么部分模型指标会无法显示,卡方、自由度也会为0,因为结构方程模型认为三个观察变量为“恰好辨识”,存在唯一解,无残差。如果只有三个观测变量,则不用考虑模型适配度的指标,只看因子载荷系数是否达标。

注:一般通过修正、调整观测模型以改善结构模型
因为整体模型适配度≈每个测量模型适配度平均,所以针对每一个潜变量和它的观测变量进行调整,以改善结构模型。调整手段参考上述两点。
具体而言,先将整体结构模型拆封为一块一块的观测模型:
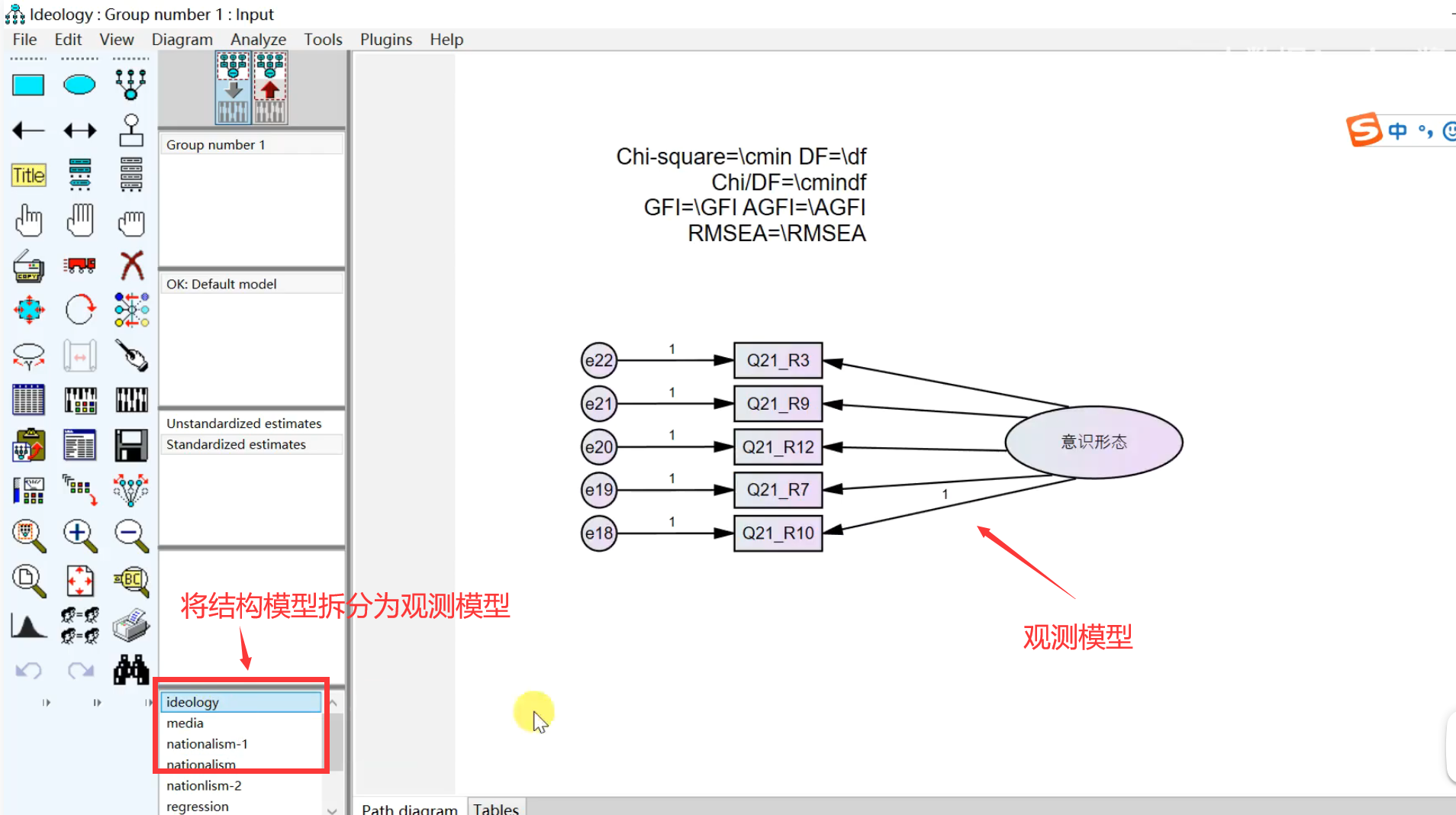
点击算盘按钮进行拟合,查看模型指标:首先看因子载荷系数或SMC是否达标,将不达标的题目删掉或残差拉相关;然后看卡方除以自由度、GFI、AGFI、RMSEA指标是否达标,将不达标的题目删掉或残差拉相关。删题目时也可以看删哪个题目对卡方的降低最多。
调整结构模型
通过收敛效度+区别效度检验,基本上结构模型就没问题了。
结构模型中,自变量需要拉相关,因为共同影响另外的一些潜变量。反过来讲,如果两个或多个潜变量共同影响另一个潜变量,那么这两个或多个潜变量应拉相关。如果这种情况没有拉相关,模型修正建议会提示拉相关后卡方值会下降。

# 路径系数分析
最后的模型结果分标准化系数和非标准化系数。这些结果在输出界面的Estimates选项卡里。
非标准化系数:判断有无显著性
在评价SEM拟合度之前,必须先通过违犯估计 Offending estimates 检查,来判定估计系数是否超出可接受范围:
- 残差项的估计系数不能为负数。
- 非标准化因子负荷量&结构路径系数需要显著。因子负荷量指的是潜变量到观测变量的路径系数。
- 自变量增加1个单位,因变量增加几个单位。
显著性仅有非标准化系数才有。标准化系数用于判断重要性。

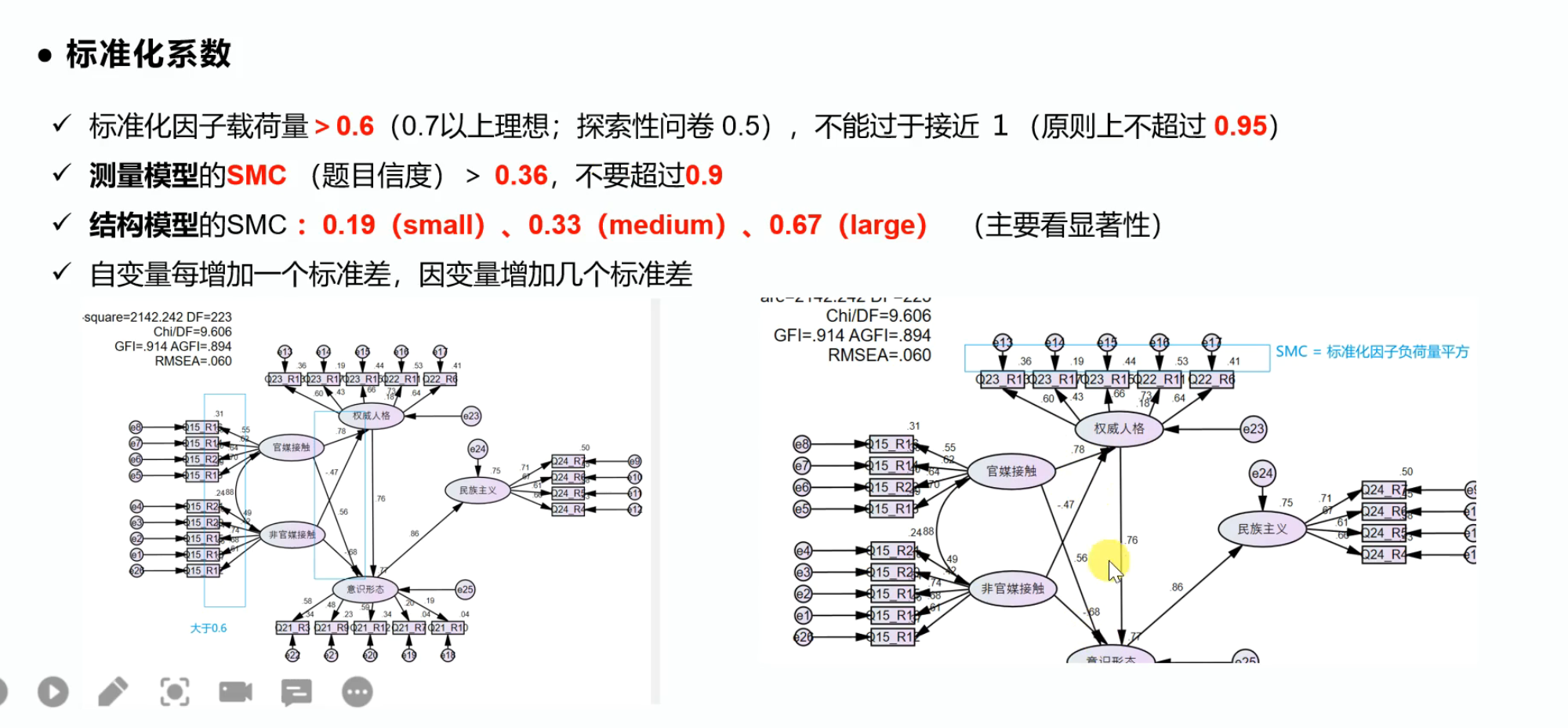
标准化系数:看重要性大小
标准化系数看以下内容:
- 标准化因子载荷量,需要大于0.6或0.5,不能过于接近1。
- 测量模型的SMC(题目信度)>0.36。
- 结构模型的SMC,先看显著性,不显著没必要解释这里的路径系数。只有显著的情况下解释路径系数才有用。若显著,这里的SMC意为重要程度。
- 自变量每增加一个标准差,因变量增加几个标准差。
潜变量之间的标准化路径系数可以用来比较重要性,而不是显著性,因为标准化系数没有显著性。
0.19为自变量对因变量的影响较小,0.33为适中,0.67为较大。
# 检验假设与分析
# 在Amos中绘制结构方程模型图
在标题栏目中给出模型评估的关键信息,这样绘图页面就能给出结果:
Chi-square=\cmin DF=\df Chi/DF=\cmindf GFI=\GFI AGFI=\AGFI RMSEA=\RMSEA
常用功能如下所示:
:将所有元素缩放至页面内。
:拉拽出一个潜在变量。
:为潜在变量增加观测变量。
:从一个潜在变量拉拽到另一个潜在变量,生成路径。
:为潜在变量或观测变量增加残差变量。
:设置标题,设置上述关键信息代码。
:选中要素。
:取消选择全部要素。
:复制要素。
:移动要素。
:更改观测变量及其残差变量的方向。
:复制要素的横纵坐标及长款等等属性,类似于格式刷。需要拖拽,点是没用的。
:如果自己画的图不好看,可以点该魔术棒。
:画完结构,导入数据之前,记得保存一下。
:从.sav文件导入数据。
:导入数据后,点击该按钮列出变量,然后将变量拖拽到对应的元素中。
:拟合结构方程模型,得到参数。
此外,双击潜变量之间的箭头以打开对象属性表,在Parameters选项卡中更改回归权重为 H1 ,以代表第一个研究假设;在Orientation复选框可以更改文字的朝向。
# 数据导入
最好先将数据导入SPSS,将数据另存为SPSS的格式。通过该格式将数据导入Amos中。在导入之前一定要做好缺失值处理,因为结构方程模型对缺失值敏感。
在Interface Properties -> Misc中,取消勾选Display variable labels,隐藏变量标签。
双击潜在变量、观测变量可以修改变量名称。值得注意的是,修改成为的变量名称不能与数据集中的变量名重复。此外,该软件对中文的识别并不友好,所以尽量将变量名填成英文。
# 模型输出&注意事项
- SEM要求中/大样本规模,至少150份样本,最好是题目:样本=1:10。
- 每个潜在变量最少对应三个观察变量,5-7个观测变量最佳。
- 每个观察变量的测量尺度颗粒度越细越好,推荐李克特7级量表。
- 整体模型的潜在变量应空值在7个以内,测量题目总共在20个左右。
- 每个观察变量一般只对应一个潜在变量。若同一个观测变量对应两个不同的潜在变量,这称为cross-loading,要求潜在变量到观测变量的路径系数>0.4。
- 相同因变量的自变量一般具有相关性,参考此处。拉不拉相关还是看模型指标。
- 每个潜在变量都需要设置1个参考指标,因子载荷量为1,剩余的为估计参数。参考此处。
- 尽量采用一阶模型,或引用经典二阶模型。二阶模型指,其中有潜变量需要通过其他潜变量来测量,其他潜变量还需要观测变量来观测的结构。这使得信息丢失率更大,整体模型适配度降低。