Statistics
# Crash Course Statistics(统计学速成)
这视频看起来花里胡哨的,需要一定基础。
# Statistics(统计学)
Mean
均值。所有数加起来求和再除以个数。
Median
中位数。将所有书从小到大排列,取最中间的数。若最中间有两个数,则取这两个数的均值。
Mode
众数。出现频率最多的数。
Range
极差。最大的数减最小的数。
Midrange
中程数。取最大值和最小值的平均数。是考虑集中趋势的又一种方式。
Pictograph
象形统计图。是用象形图像表示数据的一种方式。
Bar graph
条形图。
Line graph
线形图。可以看整体变化趋势。但要注意刻度距离和刻度数值。(横轴若为时间,则表示随时间的变化。可以是其他变量)
Pie graph
饼状图。直观反映占比。
Stem and Leaf plot
茎叶图。能一眼看出每个段有多少个体。
Box and Whiskers plot
箱线图。得到一组数值距离的散布情况和中位数。找两个四分位数(前半段的中位数和后半段的中位数)和一个中位数就能把数据分为四段。

Descriptive Statistics
描述性统计学。假设有一大堆数据,但在不希望告诉别人所有数据的情况下介绍这些数据,就可以找一些指示性的数字来代表所有的数据。而无需将所有数据都说一次。
Inferential Statistics
推论统计学。运用数据对事物作结论。只需要对样本进行一些数学计算,便可以推断出总体情况。
Discrete Variable
离散随机变量。像抛硬币,掷色子,结果是可以枚举的。
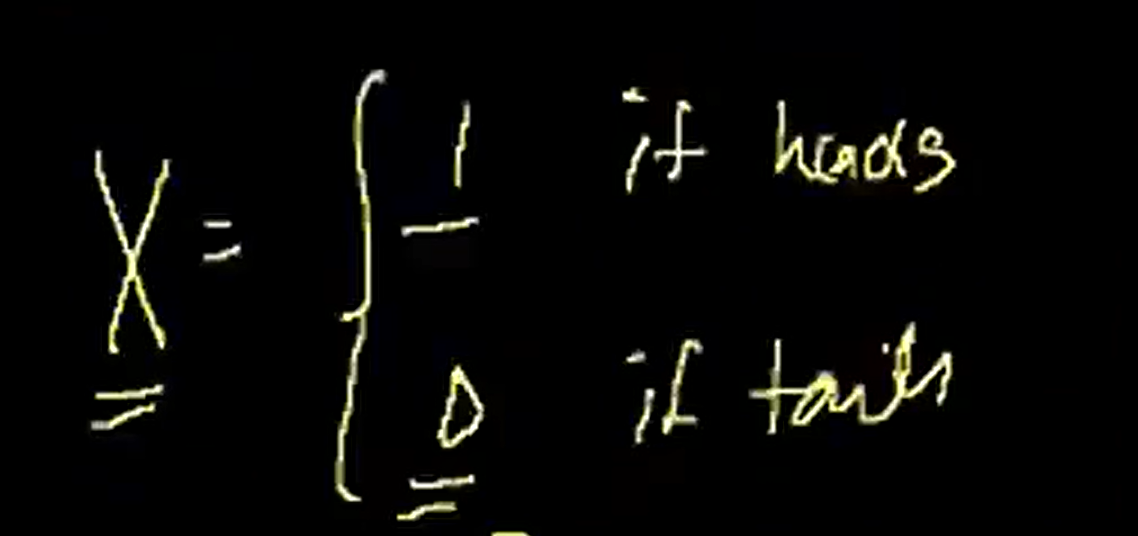
Continuous Variable
连续随机变量。结果有无数个。这种连续随机变量意味着,刚好为某个值的概率几乎为0。能算的是一个区间的概率,比如明天降雨量为1.9到2.1cm的概率就是 P(|X-2|<0.1) ,而这需要用定积分来计算。这两个随机变量的概率加起来为1。

Law of Large Numbers
大数定律。随着样本数增加,样本均值将近似于真正的期望值。
关于两个独立随机变量期望与方差的和与差的关系补充:
随机变量之差的均值=均值之差。μx-y=ux-uy。那么,μx̄-ȳ=μx̄-μȳ
两独立随机变量之差的方差=这两个变量的方差之和。Var(X-Y)=Var(X)+Var(Y)
补充这个是为了以后运用到推论统计中。有多大可能两个样本均值之差落在某一个区间内,或均值之差的置信区间是多少。
# Central Tendency(集中趋势)
最能代表数据的某个数值。
描述集中趋势的统计指标:
- 算数平均数(arithmetic mean)
- 几何平均数(geometric mean, G)
- 中位数(mean, M)
- 众数(mode)
算数均数:
适合描述对称分布资料的集中位置。


算数均数频率表例题:

组中值是(上限+下限)/2。
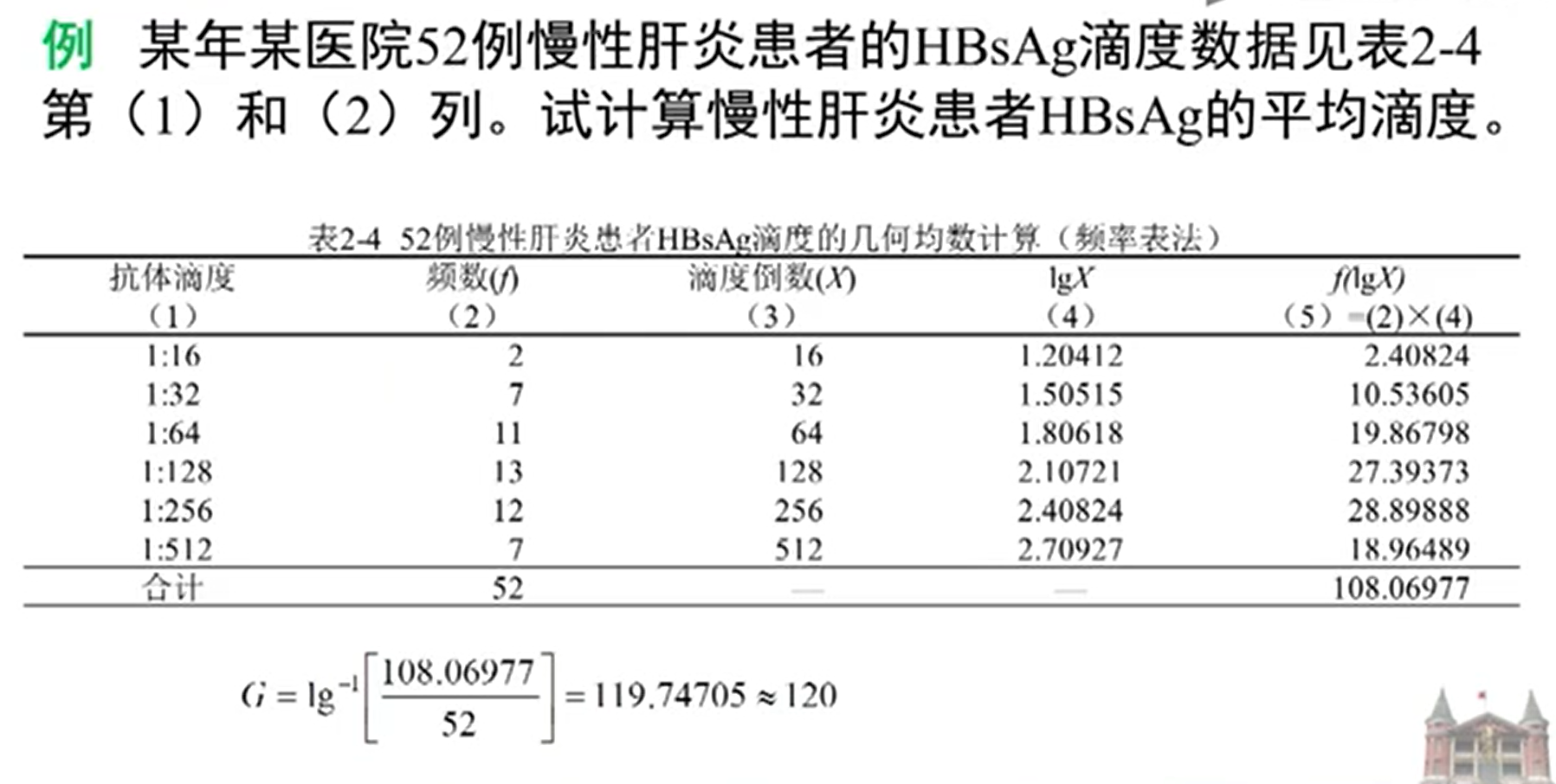
几何均数(geometric mean, G):
适用于观察值分布不对称或变化范围跨越多个数量级的资料。但经对数转换后呈对称分布的变量,如服从对数正态分布的变量。


几何均数频率表例题:
中位数(mean, M):
可用于各种分布的定量资料,特别是偏峰分布资料。
偏态分布是指频数分布不对称,集中位置偏向一侧。若集中位置偏向数值小的一侧,称为正偏态分布;集中位置偏向数值大的一侧,称为负偏态分布。
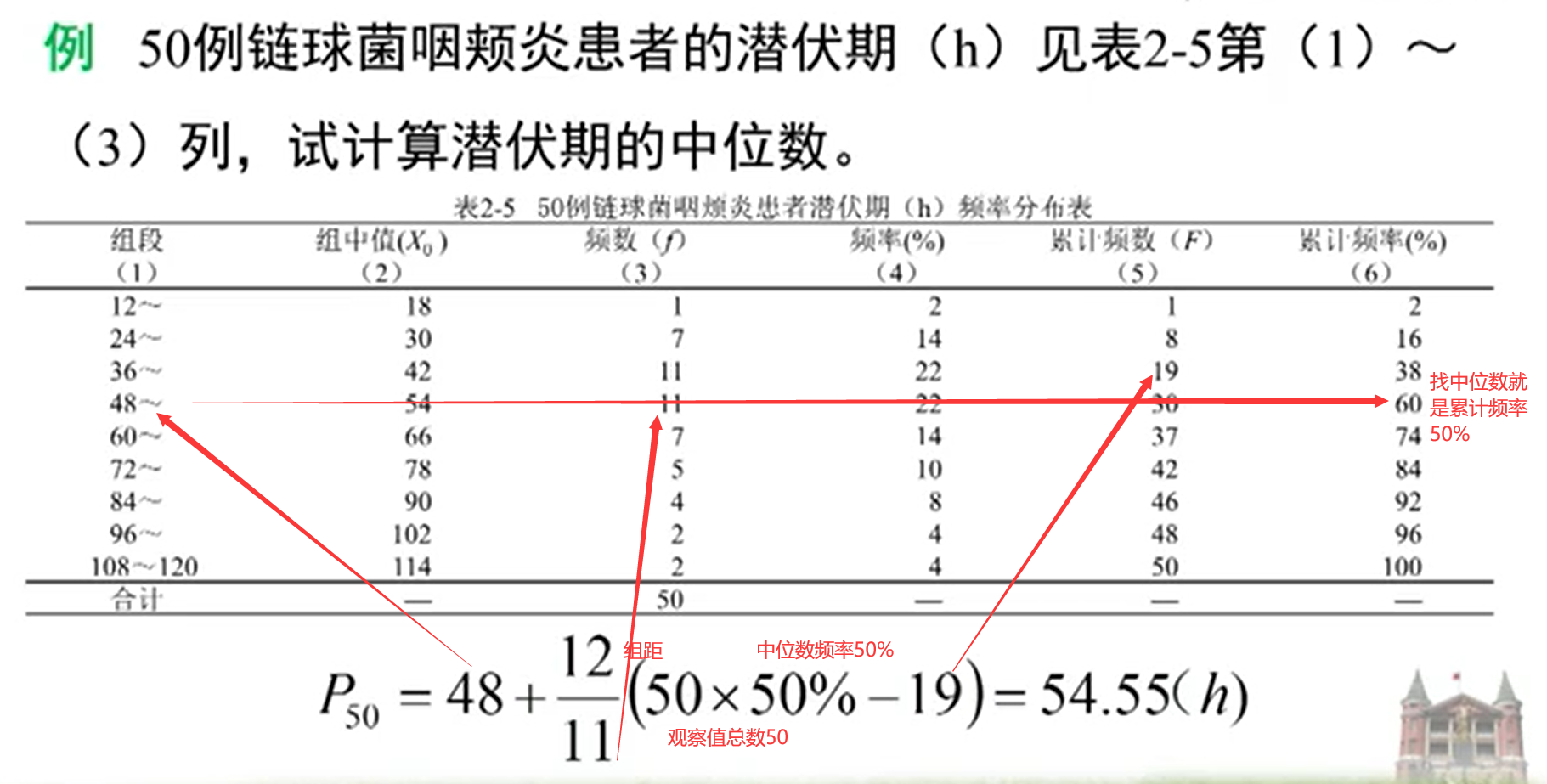
中位数也有频率表法。

中位数频率表例题:
众数(mode):
次数最多。但很少用于描述资料的平均水平。
# Dispersion(离中趋势)
Variance:
σ2方差。数据离均值的平均距离(想想几何上的距离)。
Standard Deviation:
σ标准差。用方差的话单位难免会显得很奇怪。标准差是方差开平方根。
# Population&Sample(总体与样本)
μ = population mean:
用μ这个希腊符号代表总体均值。
x̄ = sample mean:
用x̄代表样本均值。
Sample Variance(样本方差):
S2表示样本方差。由于样本取值的原因,用计算总体方差的公式计算样本方差,则计算出的样本方差通常小于总体方差。因此有一个更好的公式来进行这个总体方差的无偏估计(unbiased estimate of the population variance)或者无偏样本方差(unbiased sample variance),即S2n-1。计算方法和计算总体方差一样,但通过实验证明,除以n-1而不是n,则会更准确。所以S2与标准差(Standard Deviation)不同。
# Binomial Distribution(二项分布)
伯努利事件:独立的、可重复的、只有两个结果的事件。使用二项分布之前,得看是不是伯努利事件。
二项分布:

# Poisson Distribution(泊松分布)
泊松分布实际上来自二项分布,是二项分布的一个特殊情况,就是当观测值n取无穷大,概率p取无穷小的时候。很多人喜欢泊松分布,因为只需要一个参数λ。这个λ就相当于二项分布的np。
举个例子,在一个停车场观察了一分钟,有3辆车进来,求一分钟进5辆车的概率:
把一分钟的长度划分成n段,n趋近于无穷大,则每一段就无穷小。每一段车进来的概率为P,因为每一段时间非常短,因此P也非常小,但np=3,那么λ=3。就可以直接带进泊松分布的公式进行计算,得一分钟进5辆车的概率。

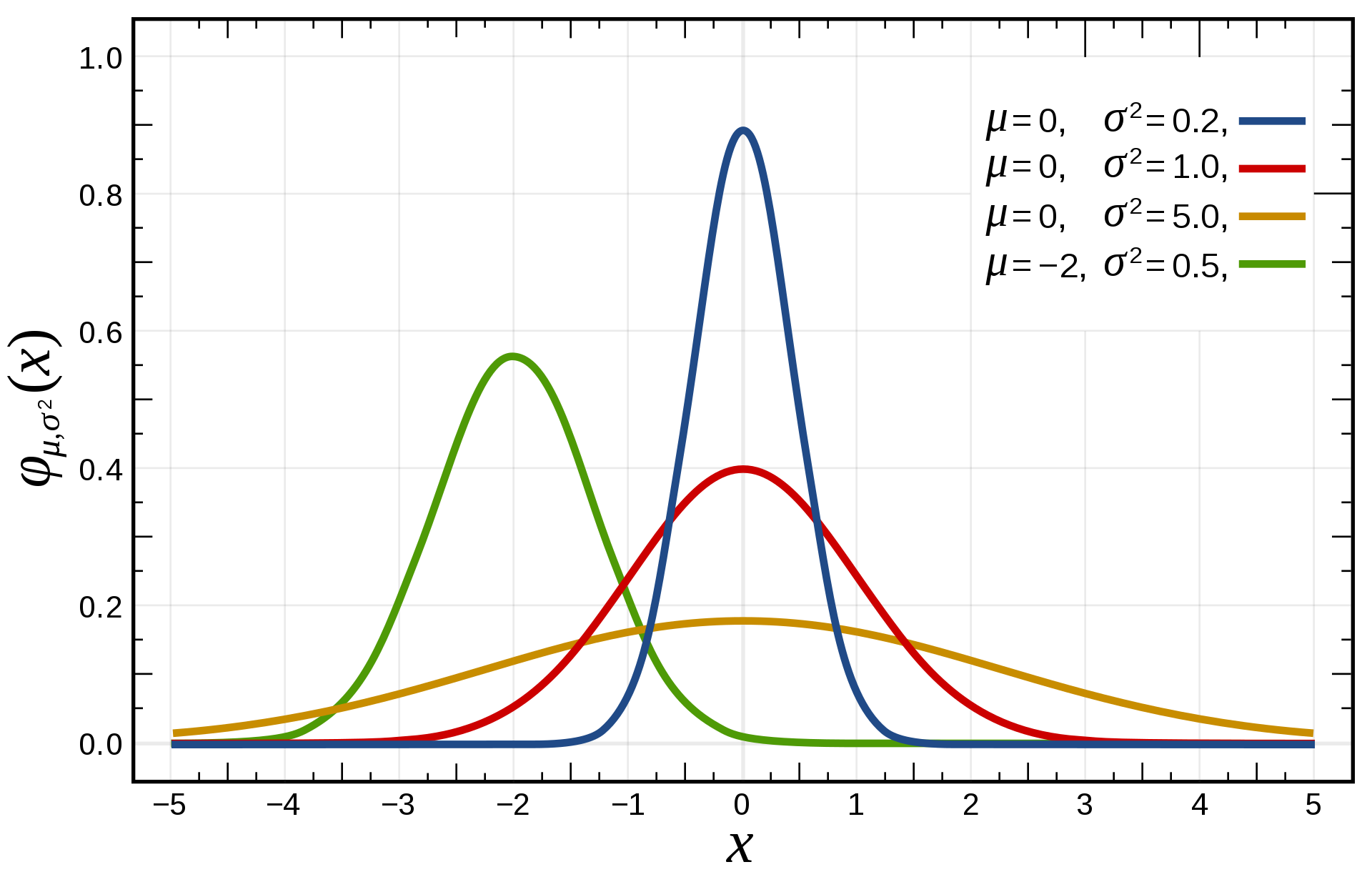
# Normal Distribution(正态分布)
正态分布,或叫高斯分布(Gaussian Distribution)、钟形曲线(Bell Curve)。推论统计几乎完全就是以正态分布为基础的,根据数据点进行推论,很大程度都是基于正态分布。其中,μ确定位置,σ确定形状。

$$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}$$
Central Limit Theorem:
中心极限定理。在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于标准正态分布。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件。
对于一个样本量足够大的随机抽样,样本均值x̄的抽样分布近似服从一个正态分布。也就是说,不管总体是服从什么分布的,可能是特别偏的分布可能是无比离散的分布,但它的样本均值的分布一定是服从正态分布的。
那么这个样本量足够大是多大呢?这和总体偏斜程度有关,越偏要求样本量越大,那么一般情况下样本量为30就够让抽样分布近似正态了。
Skewed Distribution:
偏度(skewness)也称为偏态、偏态系数,是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。
- 正偏态分布,又称右偏态分布。即平均数大于中数,中数又大于众数,则数据的分布是属于正偏态分布。正偏态分布的特征是曲线的最高点偏向X轴的左边,位于左半部分的曲线比正态分布的曲线更陡,而右半部分的曲线比较平缓,并且其尾线比起左半部分的曲线更长,无限延伸直到接近X轴。
- 负偏态分布,又称左偏态分布。即平均数小于中数,中数又小于众数,则数据的分布是属于负偏态分布。负偏态分布的特征是曲线的最高点偏向X轴的右边,位于右半部分的曲线比正态分布的曲线更陡,而左半部分的曲线比较平缓,并且其尾线比起右半部分的曲线更长,无限延伸直到接近X轴。
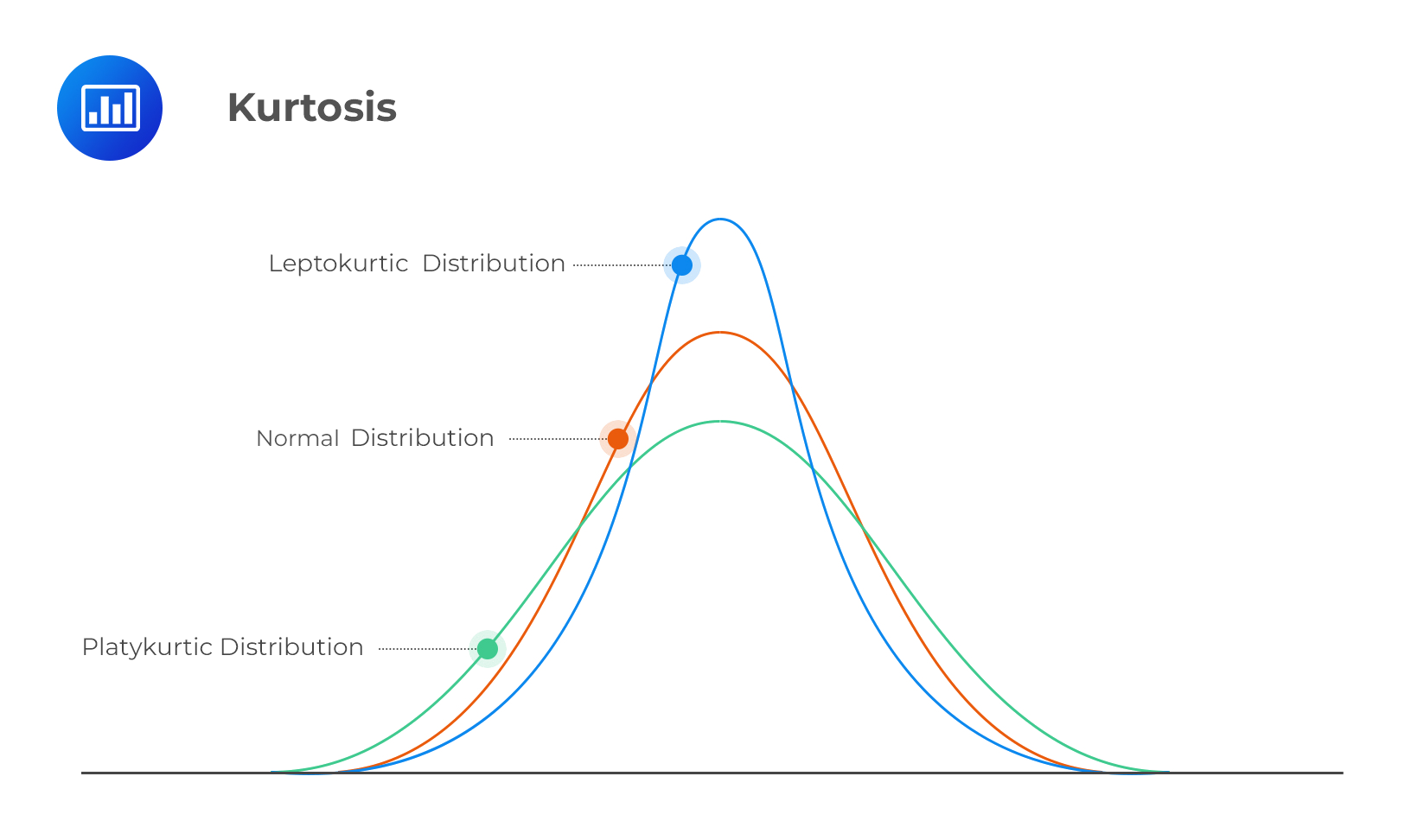
Kurtosis:
峰度,又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量,如果峰度大于三,峰的形状比较尖,比正态分布峰要陡峭。反之亦然。
Standard Score:
标准分数,也称z-score。离均值差多少个标准差 。μ是均值。虽然常用于正态分布中,但这只是指离均值差多少个标准差远,可以用在任何分布上。
。μ是均值。虽然常用于正态分布中,但这只是指离均值差多少个标准差远,可以用在任何分布上。
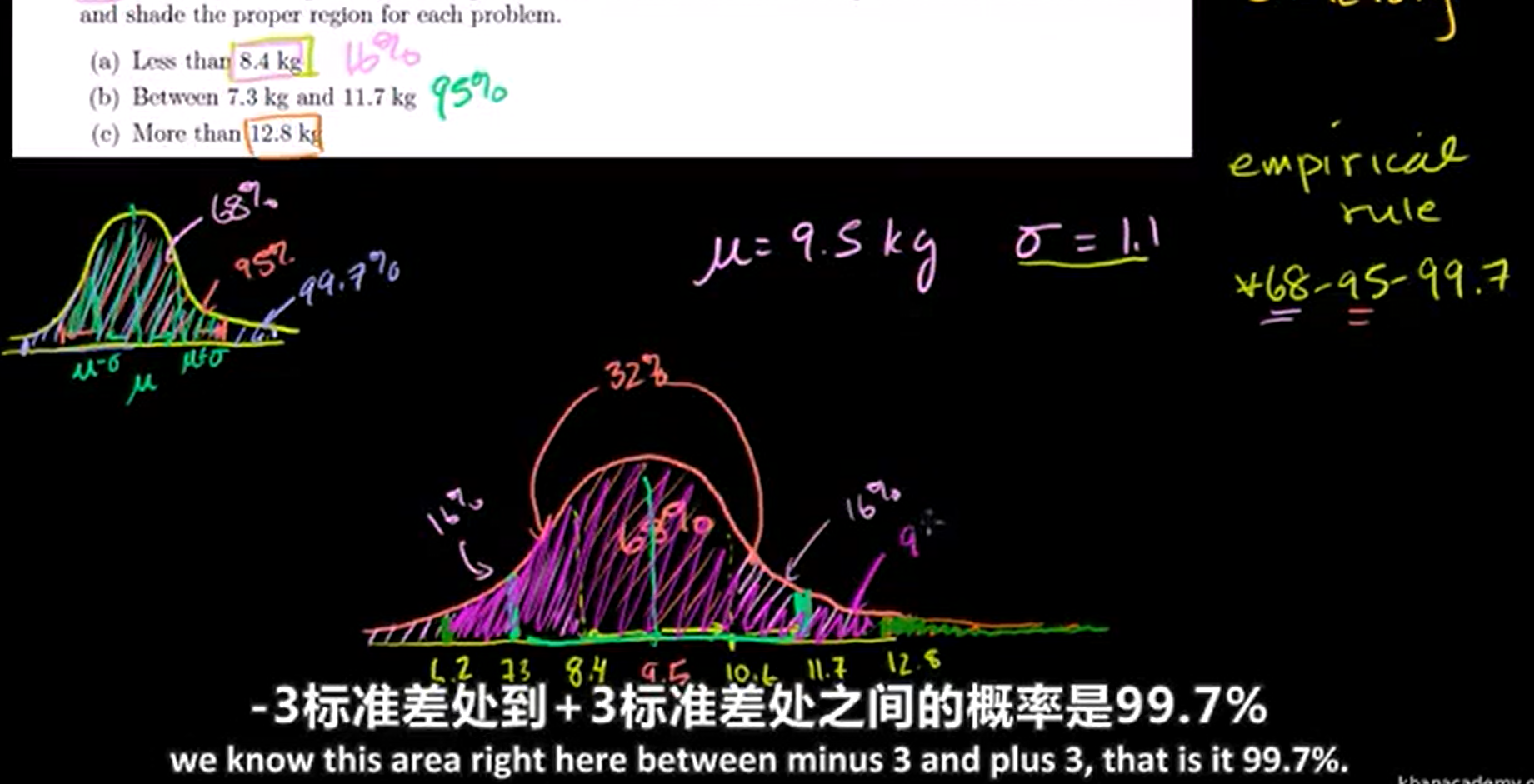
Empirical Rule(68–95–99.7 rule):
经验法则。均值左右一个标准差的概率为68%,均值左右两个标准差为95%,均值左右三个标准差为99.7%。
Standard Normal Distribution:
标准正态分布。均值μ=1,标准差σ=1的正态分布。
The Sampling Distribution of the Sample Mean:
样本均值的抽样分布。比如,一次从原分布抽取5个样本,S1就有5个样本(n=5),求这5个样本的均值,然后进行无数次这样的抽样,得到无数个抽样的均值,会发现这个抽样的均值是正态分布的。当然n不能太小。
- 原分布的方差和其样本均值的抽样分布的方差的关系是,抽样分布的方差=原分布的方差/n。
- 样本均值的抽样分布的标准差σ,就是均值标准差,也称作均值标准误差(Standard Error of the Mean)。
- n越大,均值的抽样分布的标准差越小,图像缩得越紧密。
# Bernoulli Distribution(伯努利分布)
伯努利分布是二项分布的最简单的情况。成功的概率为p,失败的概率就是(1-p)。
伯努利分布的期望和方差公式:

样本的期望和方差:
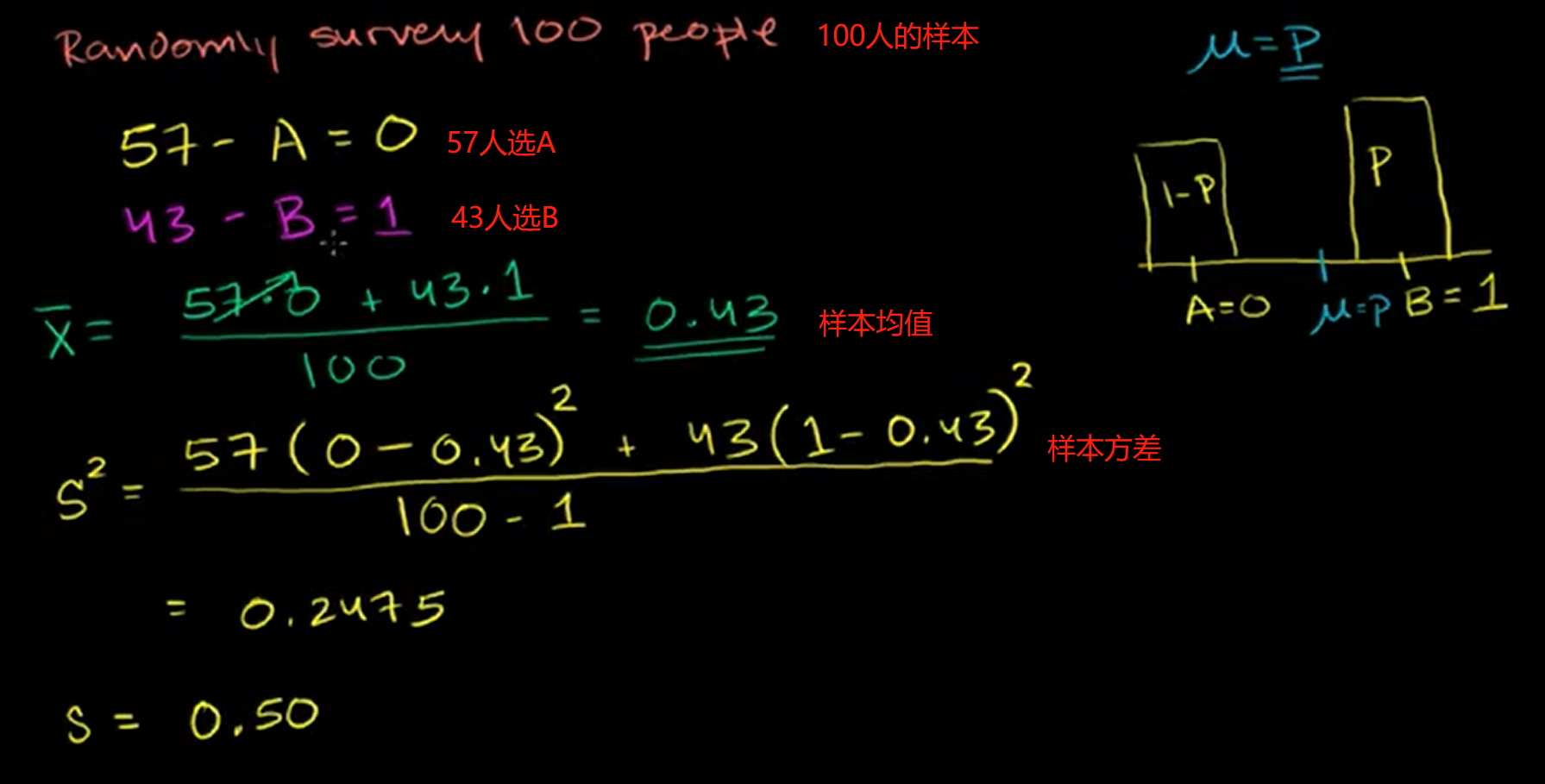
# Confidence Interval(置信区间)
2021/11/13补充:
下部分,前面用的是Z检验。后面T分布用的是T检验。Z检验与T检验区别详见配合R语言的统计学系统学习记录的统计推断部分。
置信区间是一种常用的区间估计方法,所谓置信区间就是分别以统计量的置信上限和置信下限为上下界构成的区间。对于一组给定的样本数据,其平均值为μ,标准偏差为σ,则其整体数据的平均值的100(1-α)%置信区间为(μ-Ζα/2σ , μ+Ζα/2σ) ,其中α为非置信水平在正态分布内的覆盖面积 ,Ζα/2即为对应的标准分数。

正态分布情况:
假设总体为10000人,我们不能对所有个体进行调查,则只对这10000进行一个抽样。比如抽250个人来调查。那么得到一个抽样分布,可以计算它的均值和方差。然后从这个样本均值抽样分布中抽样。这个新的抽样分布的均值等于原分布的均值,而这个新的抽样分布的标准差=原总体的标准差σ/根号下n(n为样本容量),用数学符号(注意一个是x̄一个是x)表示:σx̄=σx/√n。这个原总体标准差σ是未知的。所以用最好的估计值,所以叫置信。也就是我们有信心,实际均值在这个区间内(因为是从样本均值抽样分布中抽样,研究的是样本均值的分布)。有信心,但不是100%确信,因为用了估计值。这个σ的值是估计出来的,可以直接用样本(250个人的那个样本)标准差。

比如一个题要求计算一个99%置信区间,其中教师认为计算机是必备的教学工具。然后题干给了个250个老师的选择样本,可以计算出这个样本的均值(0.568)、方差和标准差(0.5)。从这个样本均值抽样分布中再抽样,将总体标准差估计成n为250的那个样本的标准差,就可以计算出新抽样分布的标准差(0.031)。然后通过Z score table看出如果想要99%的置信区间,那么这个样本值最远离均值多少个标准差。得到有多少个(2.58个)标准差之后,再乘以刚才估计的样本均值抽样分布的抽样的标准差。最后得出,我们相信有大概99%几率,概率P(在这里指老师认为计算机是必要教学工具的概率)落在0.568(总体均值、抽样分布的均值,它们二者相等)左右0.08(2.58*0.031)范围内。计算一下,就是说,我们相信有99%几率真实概率P在0.488到0.648之间。也就是说,我们相信有99%的几率,实际上有48.8%到64.8%的老师认为计算机是必备的。(并不是实际有这么大的几率,而是我们相信有这么大的几率)
就是说,这个置信区间,是我们有多少把握,来确定这个实际值在这个均值的多少个标准差分布里。所以实际方差是用样本标准差来估计的。我们使用样本来估计实际。所以新抽样抽的是样本的均值。
T分布情况:
不知道总体情况的时候,我们总可以使用样本标准差S来估计总体标准差σ。但如果是一个小样本容量(n=7),那么抽样分布不能像原来认为是正态分布,可以认为是T分布。T分布可以看作专门为小样本容量时置信区间的更好估计所设计的。去查T分布表,若图像关于中轴对称,则用双侧部分。单侧表示一直到特定值的累计百分比。n=7那么自由度就是n-1=6,自由度为6。举个例子,一个抽样分布(小样本)的均值为2.34,方差为1.04。通过查表可以得到当自由度为6,置信区间为95%时,对应的是2.447个标准差距离。还是将总体标准差估计为样本标准差,除以根号n,得到抽样分布的标准差。再用得到的抽烟分布标准差乘以2.447(等于0.96)。有95%几率,2.34在抽样分布实际均值周围0.96范围内,也就是总体均值周围0.96的范围内。改变一下顺序,就是,95%几率,μ也就是抽样分布均值,在样本均值2.34周围0.96范围内。
当样本容量小于30时,越小越不可能接近正态分布,所以用T分布。
t分数计算:t=(样本均值-假设的总体均值)/(样本标准差/根号下样本容量)。t分布是使用t统计量的改版正态分布。
# Statistical Hypothesis Testing(假设检验)
Null Hypothesis:
零假设,又称原假设,指进行统计检验时预先建立的假设。 零假设成立时,有关统计量应服从已知的某种概率分布。
Alternative Hypothesis:
备择假设,其包含关于总体分布的一切使原假设不成立的命题。备择假设亦称对立假设、备选假设。
一般科学方法:
假设零假设是正确的,但如果计算出该概率非常小,就可以认为零假设不正确。转而认为备择假设是正确的。
例题:
题干:分别对100只老鼠注射一单位剂量的药物,对其神经进行刺激,记录反应时间。已知没有注射药物的老鼠平均反应时间是1.2s,100只注射了药物的老鼠平均反应时间为1.05s,样本标准差为0.5s,你认为该药物对反应时间有效果吗?
解:零假设:药物对反应时间无效果。(或,注射了药物,反应时间均值仍为1.2s)
备择假设:药物有效果。(或,注射了药物,反应时间均值不再等于1.2s)。
(假设零假设是正确的,计算得到这个样本的概率,如果该概率非常非常小,则可以认为零假设不正确,于是拒绝零假设,转而认为备择假设是正确的。)
假设零假设正确:
抽样分布的均值=总体分布均值=1.2s,抽样分布标准差=总体分布标准差/根号下n=0.05。这里总体分布标准差用样本标准差来估计。
那么1.05s离抽样分布均值差3个标准差。然后参考z score table,发现得到这个极端情况的概率只有0.3%。假设零假设成立,那么只有0.3%的概率得到这个极端结果。因此在我看来,这个结果更倾向于备择假设。因此我拒接零假设,更愿相信备择假设。
注:在很多论文中,得到零假设中这种极端情况、甚至更极端情况的概率,称为p值。那么在这道题,p=0.003。通常人们会设置一个门槛,比如门槛在5%,如果p值小于5%,就拒绝假设。

Two-tailed test:
这里,我们只检验是否存在效果,不管是正效果还是负效果都被认为是有效的,这称作双侧检验。
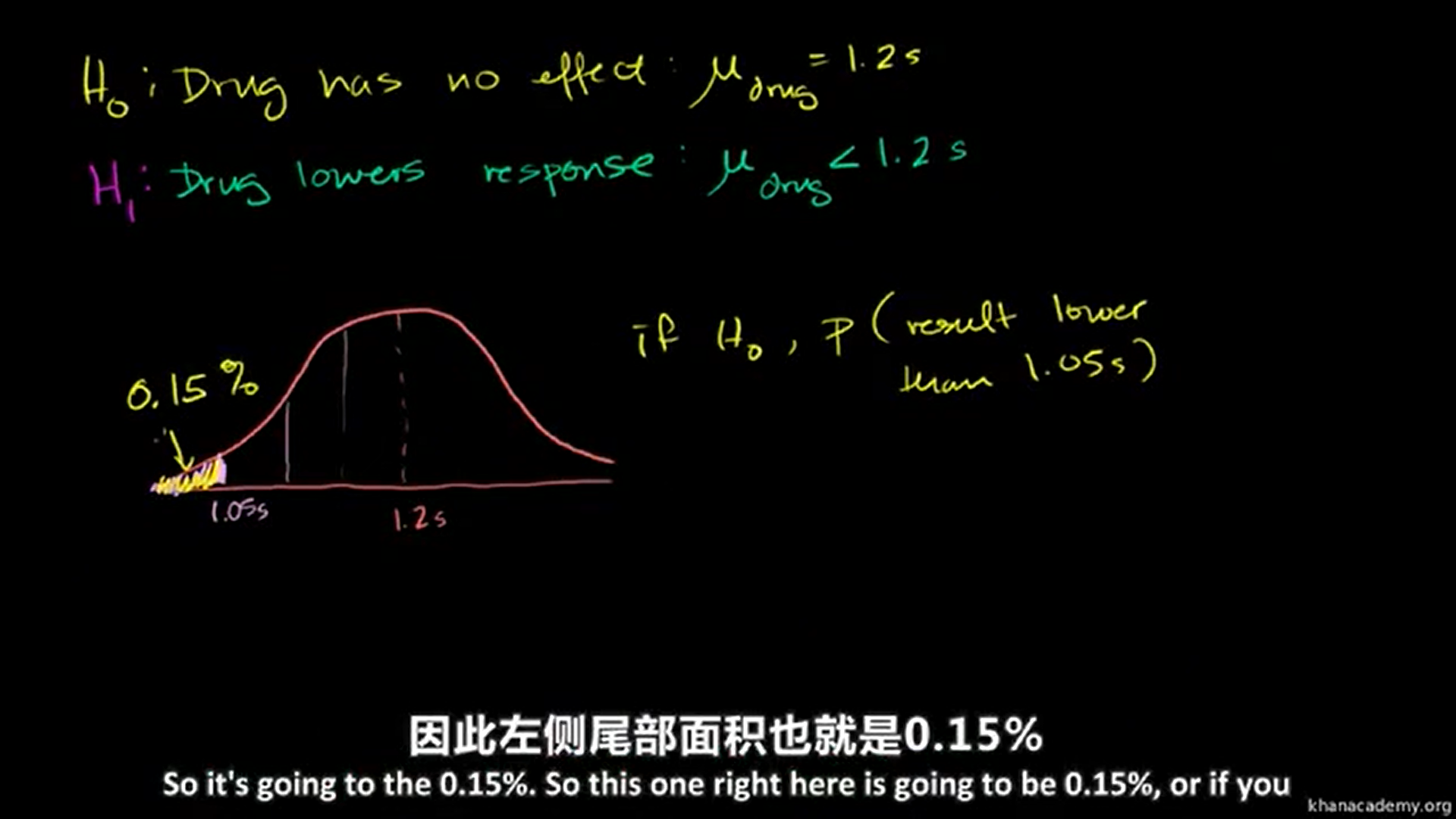
One-tailed test:
刚才做的是双侧检验。接下来做一个单侧检验。零假设:药物没有作用。备择假设:药物降低反应时间。
假设零假设正确:得到低于结果1.05s的概率只有0.15%,这非常不可能发生,所以拒绝零假设,接受备择假设。
Type 1 Error:
第一型错误。意思是拒绝了正确的零假设。比如,虽然零假设只有0.5%的概率成立,虽然很小,但仍然有几率成立。所以拒绝它可能是个错误,犯错几率是0.5%,这就是第一型错误。
# Linear Regression Equation(线性回归方程)
误差:每个点到直线的竖线距离(不是垂直距离,是竖线距离,是y的差)。

推导过程跳过,得到m和b的值的求法。

举个简单的例子:算m,算出m再算b。
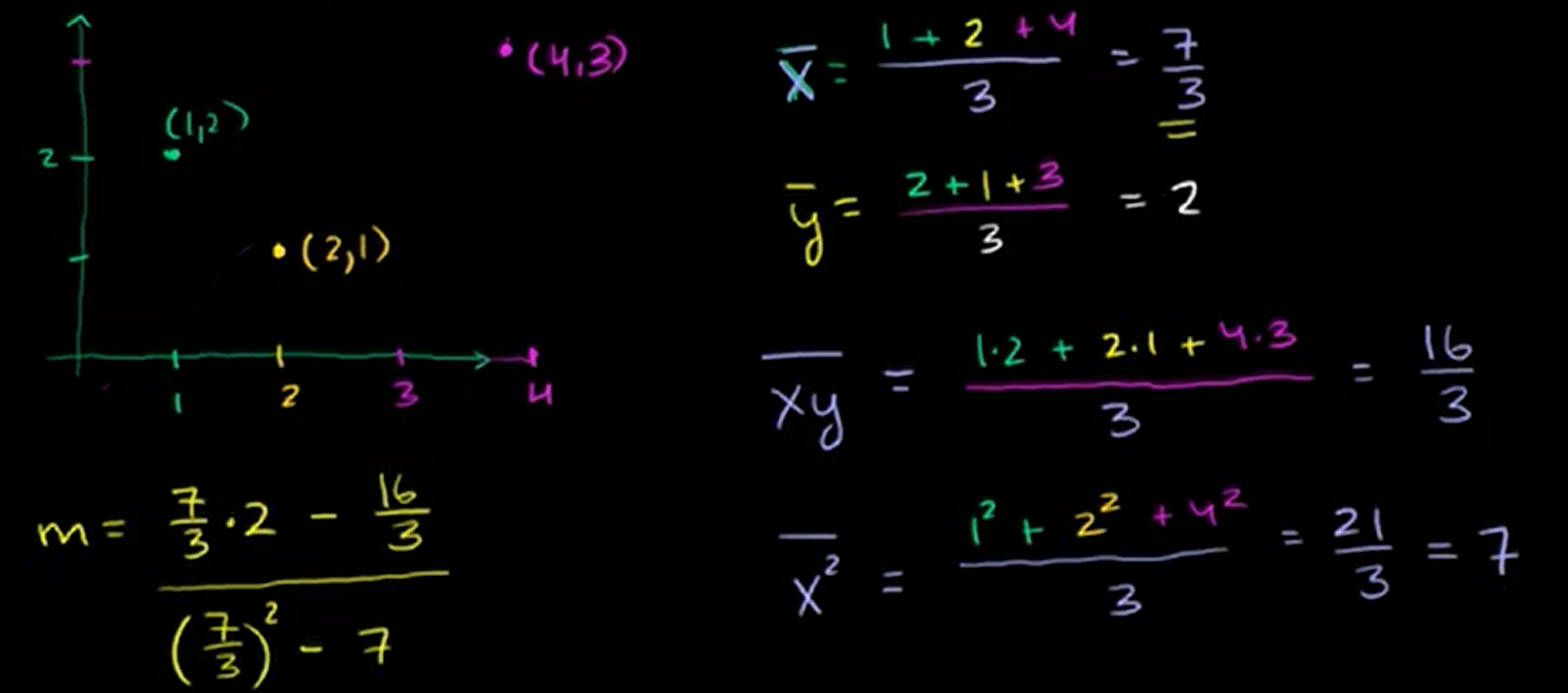
Coefficient of Determination:
决定系数,也是R2。是在线性回归的情况下,模型对观察数组的拟合程度的度量(衡量拟合的好坏)。计算公式是R2=1-(SELine/SEȳ)。R2的值不能超过1,且越接近1说明拟合得越好。
SEȳ 是所有y到ȳ的距离的平方之和。 SEȳ =(y1-ȳ)2+(y2-ȳ)2+…+(yn-ȳ)2,可以理解为y的总波动。
SELine 是所有y到回归方程的距离的平方之和,就是每一个点到直线的总平方误差(Squared Error)。 SELine =(y1-(mx1+b))2+(y2-(mx2+b))2+…+(yn-(mxn+b))2。计算R2的时候,m和b已经被计算出来了。可以直接带进去算SELine。可以理解为没有被回归线所描述的波动。
那么 SELine/SEȳ 就是总波动中,有多少百分比没有被x的波动所描述,或者说没有被回归线所描述。那么 1-(SELine/SEȳ) 就是总波动中有多少百分比被x的波动所描述,或者说被回归线所描述。
# Covariance(协方差)
协方差,在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
Cov(X,Y) = E[(X-E[X])(Y-E[Y])]
= E[XY-XE[Y]-E[X]Y+E[X]E[Y]]
= E[XY]-E[XE[Y]]-E[E[X]Y]+E[E[X]E[Y]] //因为E[X]是常数,所以E[E[X]] = E[X]
= E[XY] - E[X]E[Y]
≈ (xy)的均值-x̄ȳ //这是回归线斜率的分子部分我们回到回归线的m的公式,分子可以看作是Cov(X,Y),分母可以看作是Cov(X,X)。而方差是协方差在两个变量相同时的特殊情况(意思是Var(X) = Cov(X,X))。所以 m = Cov(X,Y)/Var(X)
# Chi-squared distribution(卡方分布)
若n个相互独立的随机变量ξ₁, ξ₂, …, ξn, 均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
它的思想是先假设数据服从某一分布或模型,然后计算出它应该有的样子,也就是期望数据。再用现实中的观察数据与之比较。算出来的χ2再去比较。

自由度:
如果只取Q=X2,那么就是1个独立的标准正态分布随机变量平方之和,那么自由度为1,Q~χ12 。如果Q=X12+x22,那么就是两个独立标准正态分布随机变量平方的和,自由度就为2,Q~χ22。有多少个随机变量自由度就为几,但如果最后一个随机变量可以又前几个随机变量求出来,那么自由度为n-1。

列联表情况:
列联表应该这样用:
- 通过观察到的数据求得总数
- 假设数据服从某一分布或模型,求出期望数据
- 有了期望数据就有了期望的占比。通过占比乘以每一组数据的总数,可以求得每一组不同类别的期望值。
- 通过期望值和观察值,求χ2
列联表经验法则:列联表有行数和列数,像下面这个表就有两行(两类别)、三列,那么自由度就是 df = (R-1)(C-1)。
下面这道题零假设是草药无效。

χ2=(20-25.3)2/25.3+(30-29.4)2/29.4+…+(90-94.7)2/94.7=2.53
接下来,比如这道题,需要去查表得到在2自由度下得到显著性水平10%的χ2统计量临界值。查表得临界值为4.6。然后和我们求得的χ2做对比。如果求得的χ2比临界值更极端,那么就拒绝零假设。如果没有那么极端,就不拒绝零假设。
2.53<4.6,所以无法拒绝零假设。也就是无法拒绝草药无效,虽然不是100%正确的,但无法拒绝。但也不能说草药有效。
# F Distribution(F分布)
F分布是两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布,是一种非对称分布,且位置不可互换。F分布有着广泛的应用,如在方差分析、回归方程的显著性检验中都有着重要的地位。
举个例子:
我们想知道这三组数据的总平方和,有多少是由于组内波动造成,有多少是由于组间波动造成。
| 一 | 二 | 三 |
|---|---|---|
| 3 | 5 | 5 |
| 2 | 3 | 6 |
| 1 | 4 | 7 |
Grand Means: 总平均值。把每组数据的所有数据都加起来,除以总数。
总的波动:简记为SST(Sum of Squares Total),也就是算所有数据点离总均值的距离的平方之和。可以将此看作是总的波动程度。自由度是 (m*n-1)
组内总波动:简记为SSW(Sum of Squares Within),求每一个成员离自己组均值的距离的平方之和。自由度是m*(n-1)
组间总波动:简记为SSB(Sum of Squares Between),求每一个组的均值离总均值的距离的平方之和。自由度是m-1
Grand Means = (3+2+1+5+3+4+5+6+7)/9=4
x̄1 = (3+2+1)/3 = 2
x̄2 = (5+3+4)/3 = 4
x̄3 = (5+6+7)/3 = 6
SST = (3-4)2+(2-4)2+(1-4)2+(5-4)2+(3-4)2+(4-4)2+(5-4)2+(6-4)2+(7-4)2 = 30 //这里有m=3组数据,每组数据有n=3个成员。那么总成员个数就是m*n=9个。自由度等于总成员数-1,也就是8个自由度。因为如果知道总均值,那么只有8个新信息。如果要计算方差的话,就是30/8。
SSW = (3-x̄1)2+(2-x̄1)2+(1-x̄1)2+(5-x̄2)2+(3-x̄2)2+(4-x̄2)2+(5-x̄3)2+(6-x̄3)2+(7-x̄3)2 = 6 //这里有m=3组数据,每组数据有n-1=2个新信息,那么自由度就是m*(n-1)=6。
SSB = (x̄1-GrandMeans)2+(x̄1-GrandMeans)2+(x̄1-GrandMeans)2+(x̄2-GrandMeans)2+(x̄2-GrandMeans)2+(x̄2-GrandMeans)2+(x̄3-GrandMeans)2+(x̄3-GrandMeans)2+(x̄3-GrandMeans)2 = 24 //自由度是组数m-1,为2
组内平方和+组间平方和=总平方和,也就是说数据中的总波动可以由每个组内的波动加上组间的波动来描述。且组间平方和的自由度加组内平方和的自由度等于总平方和的自由度。

回到F分布。那么接下来使用这些统计量,来进行一些推论统计。
先给这些数字赋予一些意义。比如,给人们吃三种不同的食物然后做测试。分为3组。那个表就是测试分数。我们想知道人们吃的食物类型是否会影响分数。毕竟从均值(x̄1, x̄2, x̄3)来看,第三组比第二组和第一组好。所以可以假设吃食物1的人的总体均值=吃食物2的人的总体均值=吃食物3的人的总体均值。因为我们有的只是样本,但肯定存在一个我们无法测量的总体均值。
零假设:均值都相,食物不会对得分产生差别。
备择假设:食物会对得分产生差别。
假设零假设成立。然后求出某统计量达到如此极端的概率是多少。那么这个统计量我们用服从F分布的F统计量。
F分布可以认为是两个χ2分布之比(两者自由度可以相等可以不相等),F-Statistics = (SSB/m-1)/(SSW/m(n-1))。
那么如果F-Statistics的分子比分母大很多,那么说明波动大多数来自于各组之间,较少来自于各组内部。那么就是一二三组每组的总体均值之间存在差异,所以F-Statistics特别大的话,说明零假设的成立概率就比较低。
如果F-Statistics比较小,说明分母比分子大,那就意味着组内波动比组间波动在总波动中占比更多,说明可能这个得分差异只是随机产生的。那么就比较难拒绝零假设。
任意假设检验都需要显著性水平,假设这里显著性水平是10%,也就是在零假设成立的情况下,如果我们计算F后得到的值小于10%的临界F值,那我们就拒绝零假设。这个临界F值是需要对应着分子分母的自由度去F表去找的。
这里分子自由度是2,分母自由度是6,对应的临界F值是3.46。那么Fc=3.46。(c是Critical的简写)
而我们计算出来的F-Statistics = (SSB/m-1)/(SSW/m(n-1)) = 12,比Fc大得多,那么零假设前提下得到如此极端的值的概率就会非常低。因此我们拒绝零假设。更偏向于相信三组分别的总体均值是存在差异的,也就是食物对得分有影响。
# Causality & Correlation(因果性和相关性)
因果性是说A导致B。
而相关性是A和B可能被同时观测到,B发生时A可能同时发生。
研究中区分因果性和相关性是非常重要的,如果是相关性就不能下结论说A导致B。好的研究是证明因果性,或者推翻文中说法的潜在因果关系,发现另一种因果关系。
# Reasoning(推理)
Inductive Reasoning:
归纳推理是一种由个别到一般的推理。由一定程度的关于个别事物的观点过渡到范围较大的观点,由特殊具体的事例推导出一般原理、原则的解释方法。自然界和社会中的一般,都存在于个别、特殊之中,并通过个别而存在。一般都存在于具体的对象和现象之中,因此,只有通过认识个别,才能认识一般。人们在解释一个较大事物时,从个别、特殊的事物总结、概括出各种各样的带有一般性的原理或原则,然后才可能从这些原理、原则出发,再得出关于个别事物的结论。这种认识秩序贯穿于人们的解释活动中,不断从个别上升到一般,即从对个别事物的认识上升到对事物的一般规律性的认识。例如,根据各个地区、各个历史时期生产力不发展所导致的社会生活面貌落后,可以得出结论说,生产力发展是社会进步的动力,这正是从对于个别事物的研究得出一般性结论的推理过程,即归纳推理。显然,归纳推理是从认识研究个别事物到总结、概括一般性规律的推断过程。在进行归纳和概括的时候,解释者不单纯运用归纳推理,同时也运用演绎法。在人们的解释思维中,归纳和演绎是互相联系、互相补充、不可分割的。
简单的说归纳推理就是寻找规律或趋势,然后推广。但不知道这个趋势是否之后是正确的。
比如有某个地区一些年份的人口数据,推理得到未来几年这个地区的人口。
Deductive Reasoning:
演绎推理则是从一些数据或事实出发,演绎得到其他正确的事实。知道这个趋势之后也是正确的。
比如推理一个等式成立,就是从一个正确的事实得到其他正确的事实。