学了四年半地信,终于搞清楚力。
# 序
本科的时候只觉得点密度分析、核密度分析做出来的图很好看。没考虑过实际作用,直到真正要用到的时候,不知所措。
# 点密度分析
执行 点密度分析 后得到的栅格图的属性值,代表的是该栅格周围某一大小的形状内某个点要素的密度。而这里的某一大小、形状、密度的单位,都是在选项卡中填入的参数决定的。
进行 点密度分析 之前,可以先将 WGS84 坐标系转为投影坐标系,以便后续进行单位的选择。在工具栏的搜索框中输入 Point Density,在 点密度分析 选项卡中,根据自身需要填入相关参数。
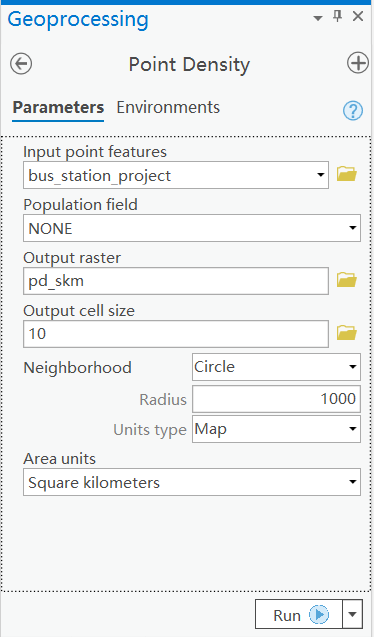
Input point features
填入想要进行点密度分析的图层。
Population field
该参数确定进行点密度分析图层里各要素的计数次数。若想每个要素只被计一次,则填入 None。
Output raster
确定输出栅格图的位置及文件名。
Output cell size
该参数确定执行点密度分析后生成的栅格图的每一个栅格的大小。若第一步的输入图层的坐标系为投影坐标系,则该栏默认单位一般来说为米。若不清楚你所使用的坐标系的默认单位是什么,可以右键内容窗口里的地图或场景,查看坐标系的默认单位(如下图所示);若第一步的输入图层的坐标系为 WGS84 坐标系,则单位为度。
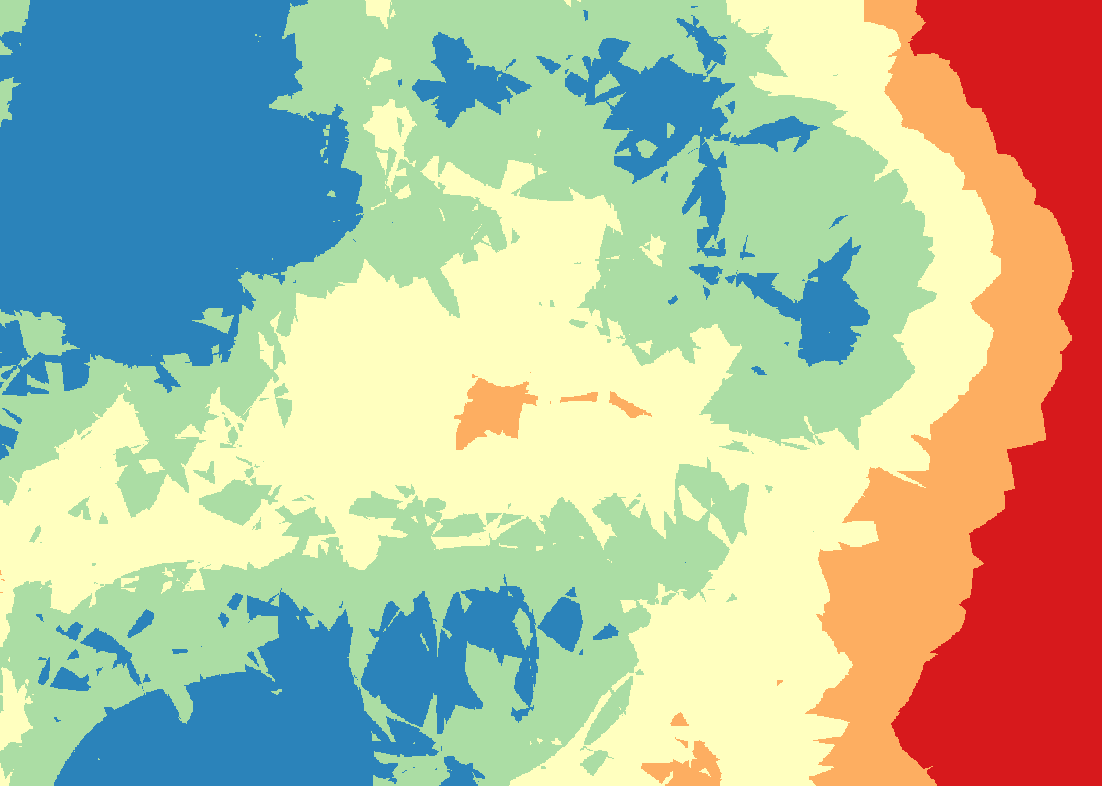
当在CGCS2000坐标系下,Cell size 设置为10时,栅格如下图所示,正如第一张图的参数所填,10米大小:
Neighborhood
可选值有矩形、圆形、环形、楔形,选择不同形状所填写的参数不同。若选圆形,则要填入Radius(半径),则点密度指的是以某一栅格为圆心,以Radius为半径画圆,在这个圆里的目标要素的密度。
Units type
字面意思为单位类型,指刚才所填入的形状参数的长度单位。有两个可选项,分别是 Map 和 Cell。
选择 Map 则长度单位与地图长度单位一致,选择 Cell 则以刚才所填写的 Cell size 为单位长度。
Area units
意思是面积单位。要理解面积单位,首先要理解——点密度分析后得到的栅格图像,每一个栅格的属性都是一个密度值(个数/面积)。
值得注意的是,若此处选择平方千米为单位,而 Neighborhood 又选择的圆形,那么在这个 Neighborhood 内的目标要素的个数除以π,才是输出栅格图的栅格属性值(个/平方千米)。
# 核密度分析
核密度分析 进行的是以四次核函数为基础的空间插值,根据单变量的样本点群,计算其空间平滑估计值。因此在结果图上可以看到要素在某个地方圆润地聚集。
计算核密度的公式
$$\large Density=\frac{1}{(radius)^2}\displaystyle\sum_{i=1}^{n}\left\lbrace\frac{3}{\pi}\times pop_i\left\lbrack1-\left(\frac{dist_i}{radius}\right)^2\right\rbrack^2\right\rbrace$$
- Density :基于四次核函数根据单变量样本群估计的密度值。
- radius :搜索半径,也称带宽。
- popi :i 点的 population 字段值,它是一个可选参数。
- disti :disti 是点 i 和 (x,y) 位置之间的距离。
搜索半径(带宽)若留空不填,则由以下公式计算得出:
$$\large SearchRadius=0.9\times \text{min}\left(SD,\sqrt{\frac{1}{\ln(2)}}\times D_m\right)\times n^{-0.2}$$
- Dm :是(加权)平均中心的(加权)中值距离。
- n :是没有使用 population 字段的点数,若使用了 population 字段,则 n 是 population 之和。
- SD :是标准距离。
- min(param1,param2) :取两个值中的较小值。
根据 population 字段的使用情况,使用不同的 SD 计算公式。
未加权时的距离
$$\large SD=\sqrt{\frac{\displaystyle\sum_{i=1}^{n}\left(x_i-\bar{X}\right)^2}{n}+\frac{\displaystyle\sum_{i=1}^{n}\left(y_i-\bar{Y}\right)^2}{n}+\frac{\displaystyle\sum_{i=1}^{n}\left(z_i-\bar{Z}\right)^2}{n}}$$
- xi, yi和zi是要素 i 的坐标。
- [x̄, ȳ, z̄]表示要素的平均中心。
- n 表示要素的总数。
加权时的距离
$$\large SD_w=\sqrt{\frac{\displaystyle\sum_{i=1}^{n}w_i\left(x_i-\bar{X}_w\right)^2}{\displaystyle\sum_{i=1}^{n}w_i}+\frac{\displaystyle\sum_{i=1}^{n}w_i\left(y_i-\bar{Y}_w\right)^2}{\displaystyle\sum_{i=1}^{n}w_i}+\frac{\displaystyle\sum_{i=1}^{n}w_i\left(z_i-\bar{Z}_w\right)^2}{\displaystyle\sum_{i=1}^{n}w_i}}$$
- [latex]w_i[/latex]是要素 i 的权重。
- [latex]\left\lbrack x_w,y_w,z_w\right\rbrack[/latex]表示加权平均中心。
# 点密度分析与核密度分析的区别
从输出结果来看。点密度分析输出的栅格图中,每一个栅格的属性值表示以该栅格为中心作出某一个大小形状的图形,落入该图形中要素的密度值。而核密度分析输出的栅格图中,每一个栅格的属性值是通过四次核函数估计的值。核密度图能平滑地反应要素本身的聚集情况。
举个例子,如果想要分析得某个区域内每个点(转为栅格)一公里内某要素的密度值,则使用点密度分析。如果想要分析某个要素的空间聚集情况,则使用核密度分析。
无论使用点密度分析还是核密度分析,都需要注意投影坐标系是否正确。如从某地图获得 gcj02 坐标系的点要素集,则需要先将它转为 EPSG4326 ,再转为合适的 Gauss-Krüger 坐标系。使用正确的投影坐标系进行点密度、核密度分析,以保证结果的准确性。