利用梯度下降求解多元线性回归参数。
# 序
梯度下降是求解最小代价的经典方法,本帖记录笔者第一次使用梯度下降求解多元线性回归的参数。
# import modules
多元线性回归的梯度下降涉及矩阵运算,因此 numpy 是必不可少的。除此之外,需要使用 pandas 输入数据到数据框中。
若想将梯度下降的过程可视化,可以借助 matplotlib 来实现,看着梯度下降的曲线非常解压。
import numpy
import pandas
from matplotlib import pyplot# data processing
数据来自Coursera-ML-AndrewNg-Notes,包括三个字段——房屋面积、卧室数量以及价格。使用 pandas.read_csv() 将数据输入到数据框中。
为提高梯度下降效率,并防止溢出,这里对输入特征进行均值归一化。由于目标变量的价格单位为一美元,这里改单位为万美元。
为使得矩阵运算正常进行,需要新增一个不存在的x0并设为1,这样使得矩阵运算时可以化为截距项。
使用 pandas.read_csv() 方法不仅读取了特征变量,还读读取了目标变量。需要将其分开方便后续计算。
最后初始化参数 theta ,因为有三个待求参数,并且之后要使用矩阵运算。所以将三个参数设为一个1×3的零矩阵。
# 数据读取
data = pandas.read_csv('ex1data2.txt', header=None, names=['Size', 'Bedrooms', 'Price'])
# Z-Score Normalization
for col in ['Size', 'Bedrooms']:
data.loc[:, col] = (data.loc[:, col] - data.loc[:, col].mean()) / data.loc[:, col].std()
data.loc[:, 'Price'] = data.loc[:, 'Price'].apply(lambda x: x / 10000)
# 构造特征值的矩阵、实际值的矩阵和参数矩阵
data.insert(0, 'ones', 1)
colNum = data.shape[1]
X = data.iloc[:, 0:colNum-1] # 这一步得到的是DataFrame
X = numpy.matrix(X.values) # 将DataFrame转为Matrix
Y = data.iloc[:, colNum-1:colNum]
Y = numpy.matrix(Y.values)
theta = numpy.matrix(numpy.zeros(3)) # 有三个参数θ待求,转换成矩阵才能参与运算# cost function
利用 numpy 的函数和方法构建多元线性回归的代价函数。
# 代价函数
def compCost(X, Y, theta):
inner = numpy.power((X * theta.T) - Y, 2)
return 1/(2*len(X))*numpy.sum(inner)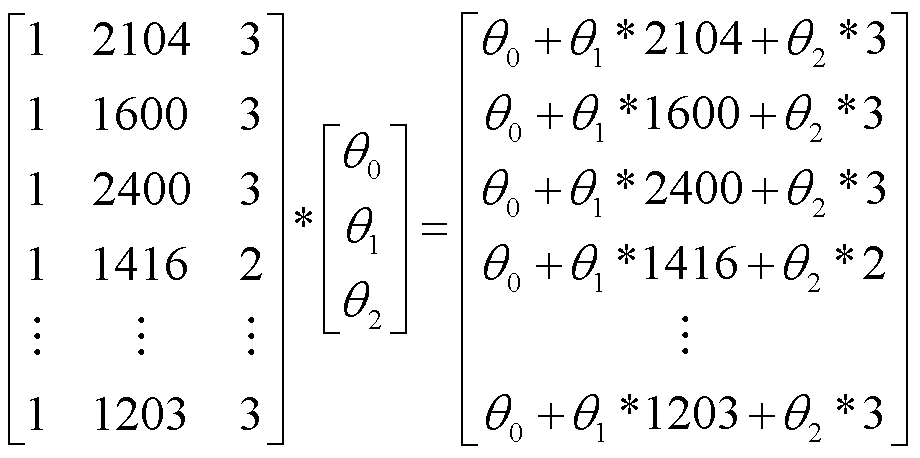
根据图像中矩阵的乘法所示,预测值矩阵应该由 X*theta.T 获得。在课程中展示的 hθ(x)=θTX 实际上是假设函数,并不是预测值的矩阵。虽然预测值矩阵是由一个一个假设函数组成,但实现过程中还是有些区别的。
# batch gradient descent
由于梯度下降时参数要同时更新,所以要再定义一个与 theta 维度一致的临时参数矩阵 temp_theta 。若想绘出梯度下降的整个过程,可以再定义一个长度为迭代次数的列表 cost 以记录每一次迭代时计算出的代价。
每一个参数按照以下公式进行梯度下降。在遍历中将新的参数输入到临时参数矩阵中,然后再进行同步更新。
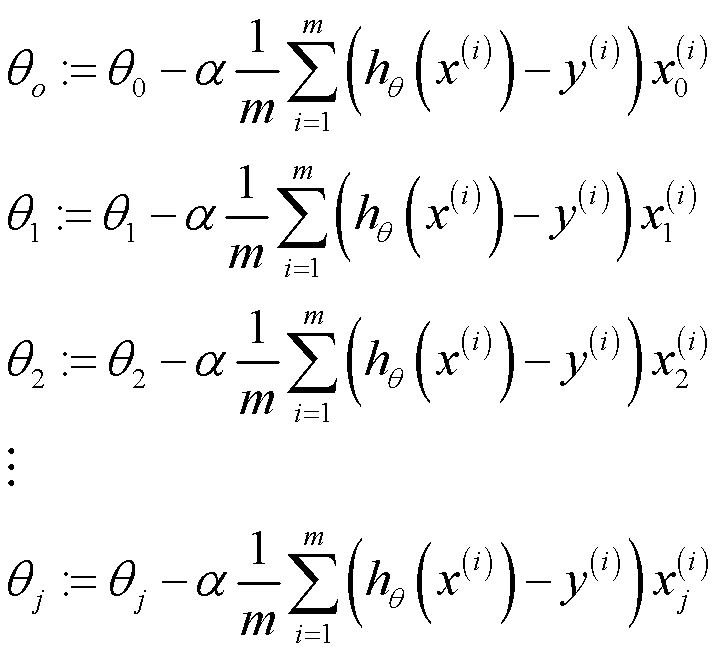
# Batch Gradient Descent Function
def batchGradientDescent(X, Y, theta, alpha, iters):
# 创建临时参数矩阵
temp_theta = numpy.matrix(numpy.zeros(theta.shape))
# 创建代价列表(ndarray)以记录每一次代价
cost = numpy.zeros(iters)
for i in range(iters):
error = X*theta.T - Y
# 计算每一个θ,并把θ添加到临时矩阵里
for nth_para, para in enumerate(theta.T):
# 每次累加中乘的x^(i)是一个标量,所以用的numpy.multiply(),而不是*
para = para - ((alpha/len(X))*numpy.sum(numpy.multiply(error, X[:, nth_para])))
temp_theta[0, nth_para] = para
# 同步更新,并记录每一次代价
theta = temp_theta
cost[i] = compCost(X, Y, theta)
return theta, cost上述代码仅定义了梯度下降的函数,接下来定义学习率和迭代次数,并进行梯度下降。
# 给定学习率、迭代次数
alpha = 0.01
iters = 1000
# 进行梯度下降
theta, cost = batchGradientDescent(X, Y, theta, alpha, iters)
# 出图
在机器学习的过程中可以产出大量十分美妙的图像,无论是分类还是预测。这里仅画出代价随迭代次数变化的图像。
# 出图
fig, ax = pyplot.subplots()
ax.plot(numpy.arange(iters), cost, 'r')
ax.set_title('Multiple Linear Regression with Gradient Descent')
ax.set_xlabel('epochs')
ax.set_ylabel('cost')
pyplot.show()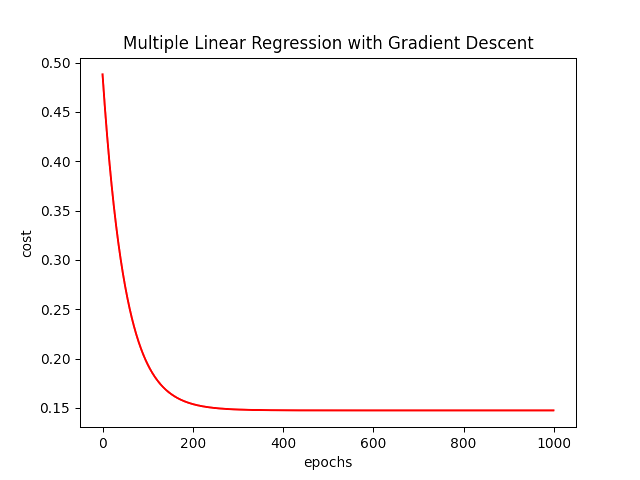
# 注意事项
在代码实现过程中,可以用数组对象来实现,也可以使用多维数组对象来实现。需要注意的是:使用 iloc[] 方法对DataFrame进行检索时只取一列数据出来,若使用 to_numpy() 函数转为数组则是一维数组,若使用 numpy.matrix(DF.values) 转为矩阵则是二维数组。后者原理就如同把一维数组 reshape() ,或理解为把一维数组转为矩阵(二维数组)。