利用梯度下降求解多项式回归参数。
# 序
表演一个过拟合的多项式回归,也可以看作是非线性回归。
# import modules
多项式回归的梯度下降涉及矩阵运算,因此 numpy 是必不可少的。在该例子中,训练集是自己创建的,不是从 Excel 中导入的,所以没有引入 pandas 。但多项式回归中次数过高,很可能会导致内存溢出,因此引入了 scikit-learn 库来执行特征缩放。
matplotlib 用于可视化梯度下降过程以及多项式拟合曲线。import numpy
from matplotlib import pyplot
from sklearn import preprocessing# data processing
数据来自2022-Machine-Learning-Specialization。先使用 numpy.arange() 创建一个特征的值,再利用特征工程的思想创建一些高次项特征,然后使用 numpy.c_[] 把新老特征合并为一个新的训练集。
该帖记录如何自己创建数据并进行特征工程,然后进行多项式拟合,展示出结果。此节记录如何自己创建训练集,并进行特征工程。
# 创建输入变量,是一个向量(或二维数组)
x = numpy.arange(0, 20, 1) # x = numpy.arange(0, 20, 1).reshape(-1, 1)
# 基于输入变量创建一个目标变量,是一个向量。为了正常运行矩阵运算,将它转为二维数组
Y = numpy.cos(x/2)
Y = Y.reshape(-1, 1)
# 特征工程,并合并为新的训练样本
X = numpy.c_[x, x**2, x**3,x**4, x**5, x**6, x**7, x**8, x**9, x**10, x**11, x**12, x**13]
# 特征缩放。若没有特征缩放,会内存溢出
scaler = preprocessing.StandardScaler()
X = scaler.fit_transform(X)
# 新增一列1,给截距项用。以便使用向量化的方案来计算代价和梯度
X = numpy.c_[numpy.ones(X.shape[0]), X]
# 创建参数矩阵,是二维数组,包括截距项b
theta = numpy.zeros((1, X.shape[1]))# cost function
该帖子用于存储训练集的对象与multiple_linear_regression_with_gradient_descent有所不同,这里用的是多维数组存储训练集,?里的帖子用的是矩阵对象存储训练集。存储对象的不同导致算法里需要采用不同的方法或计算符号来进行运算。
# 代价函数,如果用*来计算乘法,则必须有一个是矩阵。两个都是二维数组会出错,所以这里没用*来做乘法运算
def compCost(X, Y, theta):
# 因为X和Y均为二维数组,所以没有用*号来进行乘法运算
inner = numpy.power(numpy.matmul(X, theta.T) - Y, 2)
return 1/(2*len(X))*numpy.sum(inner)# batch gradient descent
梯度下降公式在 machine_learning_with_code 里有,此处不再赘述。只是由于X和Y均为二维数组, * 号乘法不再适用,改用 numpy.matmul() 函数。
# Batch Gradient Descent Function
def batchGradientDescent(X, Y, theta, alpha, iters):
# 创建临时参数二维数组
temp_theta = numpy.zeros(theta.shape)
# 创建代价列表(一维数组)以记录每一次代价,这里当作list来用
cost = numpy.zeros(iters)
for i in range(iters):
# 因为X和Y均为二维数组,所以没有用*号来进行乘法运算
error = numpy.matmul(X, theta.T) - Y
# 计算每一个θ,并把θ添加到临时参数向量里。enumerate()返回一个tuple,包含两个元素——第i行和值。
for nth_para, para in enumerate(theta.T):
# 每次累加中乘的x^(i)是一个标量,所以用的numpy.multiply(),而不是*
# X[:, nth_para]是一个一维数组,为了得到对应元素的点乘,把它转换成二维数组。
para = para - ((alpha/len(X))*numpy.sum(numpy.multiply(error, X[:, nth_para].reshape(-1, 1))))
temp_theta[0, nth_para] = para
# 同步更新,并记录每一次代价
theta = temp_theta
cost[i] = compCost(X, Y, theta)
return theta, cost上文中已经给出计算代价的函数和梯度下降的函数,接下来给定学习率和迭代次数,就可以运行基于梯度下降的多项式回归了。
# 给定学习率、迭代次数
alpha = 0.1
iters = 1000000# 出图
多项式回归可以拟合出曲线,这里使用 matplotlib 库绘出一条过拟合的曲线。
# 出图
fig, ax = pyplot.subplots(1, 2)
ax[0].plot(numpy.arange(iters), cost, 'r')
ax[0].set_xlabel('epochs')
ax[0].set_ylabel('cost')
ax[1].scatter(X[:, 1], Y)
ax[1].set_xlabel('x')
ax[1].plot(X[:, 1], numpy.matmul(X, theta.T), color='green')
# 为这两个图设置一个大标题
pyplot.suptitle('Multiple Linear Regression with Gradient Descent')
pyplot.show()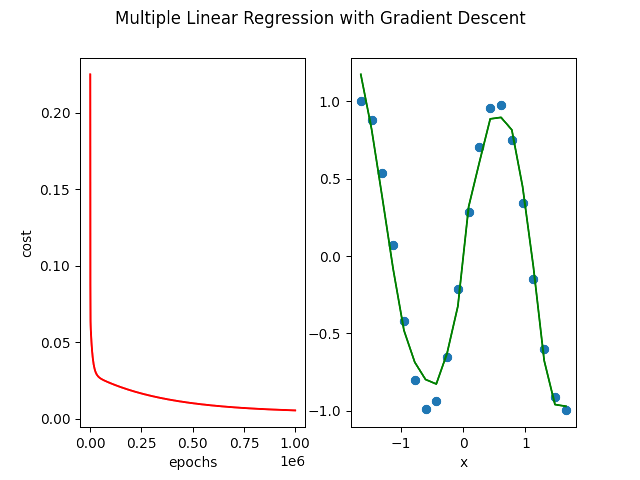
# 补充
Gradient descent is picking the ‘correct’ features for us by emphasizing its associated parameter
若在执行多项式回归梯度下降的过程中打印出每个特征的参数值,会发现可能有些特征的参数在增加,有些一直在减少。那么参数值越小意味着这个特征越不重要(或正确),如果某个特征的参数值为0或非常接近0,那么意味着该特征在拟合训练集时是 没用的东西 。
上面一段话将参数值拿来对比,是因为在数据预处理中进行了特征缩放,特征变得可比较了。