Python科学运算御用模块。
# 序
上一则帖子记录了 matplotlib 的学习历程,如果说它是 Python 的御用出图模块,那么承载大部分数学计算的 numpy 则是御用科学运算模块。
参考极客鸭geekDuckKonig的视频讲解。
# 数组
在 SIMD 的助力下, numpy 中数组的运算效率优于原始数组。因此大部分科学运算都基于 numpy 的数组实现。
创建数组
# 将list转为array
arr = numpy.array(['This', 'is', 'a', 'list'])
# 使用.arange()创建整数1到8的数组。左闭右开,步长为1。
arr = numpy.arange(start=1, stop=9, step=1, dtype=int)
# 创建由〇或一构成的矩阵,传入的tuple决定维度。
arr_zeros = numpy.zeros((1, 2, 3))
arr_ones = numpy.ones((1, 2, 3))
# 传入一个数组,返回一个维度一致,但由〇或一组成的数组。
arr_zeros_like = numpy.zeros_like(arr)
arr_ones_like = numpy.ones_like(arr)
# .identity()和.eye()都可以创建对角线为1的矩阵,前者可以创建方形的单位矩阵,后者稍微复杂点。
I_arr = numpy.identity(5)
# 查看数组的维度
print(arr.shape)
# 生成随机数,shape为(2, 3),每个元素在[0, 1)之间。
arr = numpy.random.rand(2, 3)而在出图过程中 .linspace() 与 .logspace() 最常用,前者为在一个闭区间内返回等差数组,后者则返回一个等比数列组成的数组。
# 创建0~100内(闭区间)由5个数组成的等差数组
arr1 = numpy.linspace(1, 100, 5)
# 在10^0~10^2内(以10为底,闭区间)由5个数组成的等比数组
arr2 = numpy.logspace(0, 2, 5, endpoint=True, base=10)更改数组维度
# 创建1~24组成的数组
arr = numpy.arange(start=1, stop=25, step=1)
# 更改为2维数组(形似矩阵)
arr = arr.reshape(4, 6)
# 更改为3维数组
arr = arr.reshape(3, 4, 2) # 值得注意的是,第一个维度变化得最慢,往后越来越快。很抽象,可以跑个代码看下结果。
# 合并所有维度,转化为(n, )的一维向量
arr = arr.flatten()
# 去除冗余维度,比如下面的1就是冗余的。
arr = numpy.zeros((1, 4, 2))
arr = numpy.squeeze(arr)
# 交换数轴。把第一个轴和第二个轴交换,从2行3列变成3行2列
x = numpy.array([[1, 2, 3], [4, 5, 6]])
x = numpy.swapaxes(x, 0, 1)
# 二维数组转置,shape从(2, 3)变为(3, 2)
arr = numpy.zeros((2, 3))
arr = arr.transpose() # 等同于arr.T
# 多维数组调换每个轴出现的位置。shape从(4, 5, 6)变为(5, 4, 6)
arr = numpy.zeros((4, 5, 6))
arr = arr.transpose((1, 0, 2)) # 将第二个轴排第一位,第一个轴排第二位,第三个轴排第三位。数组的拼接
用于拼接的函数主要为 concatenate() 与 v/h/dstack() ,前者可用于在存在的任意维度的拼接,后者在二维上仅限于竖着 dimension 0 、横着 dimension 1 和depth-wise dimension 2 拼接,在多维上也仅限于在第0、1、2维上拼接。接下来分二维情况、多维情况与一维情况举例,首先是二维数组的情况:
arr1 = numpy.zeros((2, 3))
arr2 = numpy.zeros((1, 3))
arr3 = numpy.zeros((2, 5))
arr4 = numpy.zeros((2, 3))
# 竖着拼接arr1与arr2,新数组shape为(3, 3)
# 除了连接轴之外,所有输入数组的shape都必须完全匹配
numpy.vstack((arr1, arr2))
numpy.concatenate((arr1, arr2), axis=0)
# 横着拼接arr1与arr3,新数组shape为(2, 8)
numpy.hstack((arr1, arr3))
numpy.concatenate((arr1, arr3), axis=1)
# depth wise拼接,新数组shape为(2, 3, 2)。因为原数组为二维数组,concatenate()函数找不到第三个维度的数轴,而dstack()将(m, n)的维度升到了(m, n, 1),便有了第三个数轴。
a = numpy.dstack((arr1, arr4))多维数组的情况:
arr1 = numpy.zeros((1, 2, 3, 4))
arr2 = numpy.zeros((3, 2, 3, 4))
arr3 = numpy.zeros((1, 3, 3, 4))
arr4 = numpy.zeros((1, 2, 5, 4))
arr5 = numpy.zeros((1, 2, 3, 9))
# 在dimension 0上拼接(shape的第一项),新数组shape为(4, 2, 3, 4)
# 除了连接轴之外,所有输入数组的shape都必须完全匹配
numpy.vstack((arr1, arr2))
numpy.concatenate((arr1, arr2), axis=0)
# 在dimension 1上拼接(shape的第二项),新数组shape为(1, 5, 3, 4)
numpy.hstack((arr1, arr3))
numpy.concatenate((arr1, arr3), axis=1)
# 在dimension 2上拼接(shape的第三项),新数组shape为(1, 2, 8, 4)
numpy.dstack((arr1, arr4))
numpy.concatenate((arr1, arr4), axis=2)
# 在dimension 3上拼接(shape的第四项),新数组shape为(1, 2, 3, 13)
numpy.concatenate((arr1, arr5), axis=3)总的来说,除了遇到一维数组的情况, v/hstack() 的作用分别与 concatenate(, axis=0/1) 一致。具体而言,遇到一维数组 1d-array 时:
arr1 = numpy.array([1, 2, 3]) # shape(3,)
arr2 = numpy.array([4, 5, 6]) # shape(3,)
arr3 = numpy.array([[11, 22, 33], [44, 55, 66]]) # shape(2, 3)
# vstack()将认为一维数组的shape为(1, n),等价于concatenate((1darr.reshape(1, n), arr2), axis=0)
numpy.vstack((arr1, arr3))
numpy.concatenate((arr1.reshape(1, len(arr1)), arr3), axis=0) # 与上式等价
# hstack()将不再作用于dimension 1,而作用于dimension 0,等价于concatenate((1darr, arr), axis=0)
a = numpy.hstack((arr1, arr2))
b = numpy.concatenate((arr1, arr2), axis=0) # 与上式等价总之,在遇到一维数组时最好按照需求将它转为合适的维度,再使用 concatenate() 函数进行拼接。
此外, dstack() 与将(m, n)的二维数组升维至(m, n, 1)、(n, )一维数组升维至(1, n, 1)的 concatenate(, axis=2) 作用一致。
进一步而言,对还有 numpy.c_[] 与 numpy.column_stack() 这两个方法对一维数组有特殊效果。在特征映射中这两个方法减少了复杂工作。
a = numpy.array([1, 2, 3])
b = numpy.array([4, 5, 6])
c = numpy.array([7, 8, 9])
d = numpy.array([[1, 4], [2, 5], [3, 6]])
# 将切片对象转换为沿第二个轴的拼接。若遇到一维数组,会先将其shape转为(-1, 1)后再拼接。
numpy.c_[a, b, c, d]
# 获取一系列一维数组并将它们堆叠为列以形成单个二维数组。二维数组按原样堆叠,就像hstack()一样。一维数组首先变成二维列。
numpy.column_stack((a, b, c, d))
# 用法见上文
numpy.hstack((a.reshape(-1, 1), b.reshape(-1, 1), c.reshape(-1, 1), d.reshape(3, 2)))
'''
[[1 4 7 1 4]
[2 5 8 2 5]
[3 6 9 3 6]]
'''stack() 函数的用途为沿着一个新的轴堆叠维度相同的一系列数组,返回数组维度会比传入的数组多一个维度,同时要求两个传入的数组维度相同。该函数的用途和条件与上面的拼接函数差别较大。数组的堆叠
数组的选取
# 截取一些元素
# 截取到的arr_的维度为(2, 1, 1)
arr = numpy.arange(1, 25)
arr = arr.reshape((2, 3, 4))
arr_ = arr[:, :1, :1]
# 获取对角线的元素
arr = numpy.array([[1, 2, 3], [4, 5, 6]])
arr_ = numpy.diag(arr)
# 选取某个元素
arr_ = arr[1][2] # 选择第2行第3个元素,为6
# 给定两个列表分别确定所要选取元素所在的行列
arr_ = arr[[0, 1], [0, 2]] # 选取第1行第1列和第2行第3列的两个元素
# 获得1、2行的第2、3列所有元素
arr_ = arr[[0, 1], :][:, [1, 2]]arr = numpy.array([[1, 2, 3], [4, 0, 6]])
# 用法i:根据条件替换值。保留所有大于等于5的值,其余值替换为0
arr = numpy.where(arr >= 5, arr, 0)
# 用法ii:根据条件返回值的索引的元组。.argwhere()则返回索引组成的列表
index_tuple = numpy.where(arr >= 5)
# 根据索引的元组来选择这些值
arr_ = arr[index_tuple]
arr_ = arr[arr >= 5] # 与上一行代码实现相同的效果,输出的是数值而不是索引对于 numpy 中的特殊值 NaN 与 inf ,则需要配合 .isnan() 或 .isinf() 函数来选取,而不能直接用 == 来选取。
arr = numpy.array([-1, 0, 1])
log_arr = numpy.log(arr)
'''
log_arr is [ nan -inf 0.]
'''
index_tuple = numpy.where(log_arr == numpy.inf) # 错误的
index_tuple = numpy.where(numpy.isinf(log_arr)) # 正确的数组运算
首先明确 numpy 中有以下变量:
# 非数
numpy.nan
# 无穷数
numpy.inf
# 圆周率
numpy.pi
# 自然常数
numpy.e
# 空数轴
numpy.newaxis
# 关于空数轴
arr = numpy.zeros((4, 5, 6))
arr1 = arr[numpy.newaxis, :, numpy.newaxis, :, :]
'''
(1, 4, 1, 5, 6)
'''
arr2 = arr.reshape(1, 4, 1, 5, 6) # 等价对每个元素进行加减乘除运算:
arr = numpy.zeros((4, 5, 6))
# 加法
arr + 1
# 减
arr - 1
# 乘
arr * 2
# 除法
arr / 2其他常见的运算函数:
# EXP
numpy.exp(arr)
# sin, cos
numpy.sin(arr)
numpy.cos(arr)
# 乘幂
numpy.power(arr, 2) # 等价于arr^2
# 求和运算
arr = numpy.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
# 对每一列进行求和,并返回每一列求和后的值的一维数组。axis=0意味对于除dimension 0外的所有元素,求对应dimension 0位置上所有元素的和。
col_sum = numpy.sum(arr, axis=0)
# 对每一行进行求和,并返回每一行求和后的值的一维数组
row_sum = numpy.sum(arr, axis=1)
# 对每一列进行求和,并返回由每一列每次累加值结果组成的多维数组。
col_cumsum = numpy.cumsum(arr, axis=0)
# 对每一行进行求和,并返回由每一行每次累加值结果组成的多维数组
row_cumsom = numpy.cumsum(arr, axis=1)
print(col_cumsum)
'''
[[ 1 2 3 4]
[ 6 8 10 12]
[15 18 21 24]]
'''
print(col_cumsum.shape)
'''
(3, 4)
'''
print('---')
print(row_cumsom)
'''
[[ 1 3 6 10]
[ 5 11 18 26]
[ 9 19 30 42]]
'''
print(row_cumsom.shape)
'''
(3, 4)
'''多维数组、一维数组(向量)的乘法运算:
vec1 = numpy.array([1, 2, 3])
vec2 = numpy.array([2, 3, 4])
vec3 = numpy.array([5, 6])
vec4 = numpy.array([[1, 2, 3], [4, 5, 6]])
vec5 = numpy.array([[1, 5, 9], [2, 4, 8]])
# 相同shape则按位置相乘
vec4 * vec5
'''
[[ 1 10 27]
[ 8 20 48]]
'''
# 两个一维向量内积,.dot()可以替换为@
numpy.dot(vec1, vec2) # 20
# 两个一维向量外积
numpy.outer(vec1, vec2)
'''
[[ 2 3 4]
[ 4 6 8]
[ 6 9 12]]
'''
# 矩阵乘法
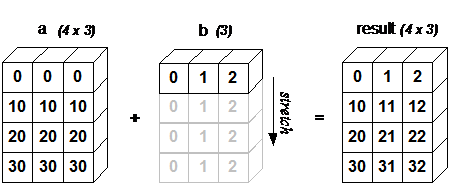
numpy.dot(vec4, vec5.T)Broadcast
在维度为1的地方补全元素以完成运算
过滤-Filter
创建Boolean List实现过滤。需要注意的是Boolean list的维度,当它的维度为(m,)时,它可以被用来过滤(m,n)的数组;而当它维度为(m,1)时,它只能被用来过滤(m,1)的数组。可见,除前者情况,Boolean list和被过滤数组维度需要相同,可以手动更改Boolean list的维度和每一个布尔值。
arr = numpy.array([[1, 2, 3], [4, 0, 6]])
# 创建Boolean list
arr_ = arr >= 5
print(arr_)
'''
[[False False False]
[False False True]]
'''
# 除大于等于5的元素,还想要第一列
arr_[:, 0] = True
'''
[[ True False False]
[ True False True]]
'''
arr_filtered = arr[arr_]
'''
[1 4 6]
'''
# 多个条件
arr_filtered = arr[(arr > 1) & (arr < 3)]
arr_filtered = arr[((arr > 1) & (arr < 3)) | ((arr > 5) & (arr < 7))]
通过 numpy.where() 函数实现数组过滤。
arr = numpy.array([[1, 2, 3], [4, 0, 6]])
# index of elements to keep
index_to_keep = numpy.where(arr >= 5)
# filter the array
arr_ = arr[index_to_keep]
# 多个条件
arr = numpy.array([[1, 2, 3], [4, 0, 6]])
index_to_keep = numpy.where((arr > 1) & (arr < 3))
index_to_keep = numpy.where(((arr > 1) & (arr < 3)) | ((arr > 5) & (arr < 7)))
arr_ = arr[index_to_keep]数组内行列的删除
通过 numpy.delete() 函数实现数组内行列的删除。
# arr为待删除的数组;obj为切片、整数或整数的列表;axis为数轴,根据shape确定axis。当axis=0时意味shape中第一个数字占的数轴
numpy.delete(arr, obj, axis=None)
# 删除x1二维数组第3列
x1 = numpy.delete(x1, 2, axis=1)
# 删除x2二维数组第1和第2行
x2 = numpy.delete(x2, [0, 1], axis=0)# 数值类型
在使用 python 编程时就没注意过定义数据类型了,因为它可以自动转换,很方便。以下代码是使用 numpy 查看数据类型和强制转换类型:
arr = numpy.array([1, 2, 3])
# .dtype是属性
print(arr.dtype)
# 强制转换数值类型
arr = arr.astype(numpy.float64)
arr = arr.astype(int)
arr = arr.astype(numpy.bool_)
# 更多数据类型查看 - https://numpy.org/doc/stable/user/basics.types.html# 随机数
使用 .random.rand() 可以创建 [0, 1) 的随机数,而 .random.randn() 是从标准正态分布中返回一个或多个样本值,即这些随机数的期望为〇,方差为1。
.random.seed() 用于生成指定随机数。具体为先用该函数指定从哪个堆里取随机数,如果有从同一个堆里取随机数,那么取随机数之前需要指定这个堆,否则生成的随机数将不同。numpy.random.seed(3)
print(numpy.random.rand(1, 5))
time.sleep(1)
numpy.random.seed(3)
print(numpy.random.rand(1, 5)) # 与上一次生成的随机数相同
numpy.random.seed(3)
print(numpy.random.randn(1, 5))
print(numpy.random.randn(1, 5)) # 与上一次生成的随机数不同# meshgrid()
返回决定所有网格点的每个坐标系上的位置矩阵,作用如下图所示:

若第一个参数的维度为(n,),第二个参数的维度为(m,),那么由函数 X, Y = numpy.meshgrid(x, y) 返回的两个矩阵 X, Y 表示的网格点如下:
