GeoDetector。
# 序
GeoDetector 能够检验目标变量是否存在空间分层异质性,并得到不同变量及其两两交互的变量对目标变量的解释力。# 空间分层异质性
空间分层异质性(Spatial Stratified Heterogeneity, SSH),简称空间分异性。该词想表达的意思是,在空间的不同层(区)变量之间的关系不同。也就是说,不满足经典统计学的同分布假设。因此推出地理探测器,在考虑到空间分层异质性的情况下探讨输入变量与结果变量之间的关系。
# 度量空间分层异质性
地理探测器计算出的一个结果是 q-value ,且 q∈[0,1] ,该值若为0,则目标变量不存在空间分异,该值越大则越说明目标变量存在空间分异。
q-value
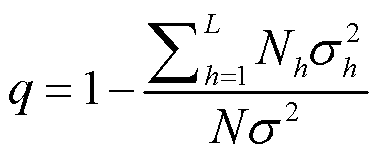
计算出的 q-value 是解释力,若为0.23,则能解释23%。
q-value的一个简单变换满足非中心F分布
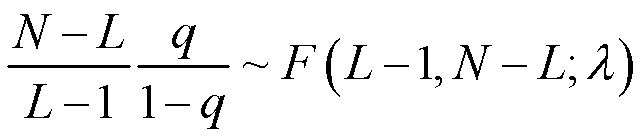
# 空间分层异质性归因
数据驱动很难拿来归因,因为有相关关系不代表因果关系。但数据驱动加其它信息,拿来归因也可以被认可。地理探测器的结果可以强烈地提示存在因果关系,因为额外给出了空间上的关系。
# 地理探测器故事
这九个故事也是地理探测器的九个实际运用方式。
Test SSH: Existence of Spatial Pattern
检测某个结果变量是随机分布的还是有一定规律性分布。
Find SSH, then Modelling in Strata
某些经典算法要求变量具有同一规律,如克里金插值有二阶平稳假设。那么可以先找到不同的分层(区),再针对每个层运用该经典算法。
Determinants’ Spectrum
找因子谱,得到每个变量对结果变量的解释力。如在某个研究中发现流域对某疾病发病率的解释力高达47%。
Determinants’ Spectrum, in Regions
根据因子谱根据空间的变化来讲故事。先根据已有的区域(定性、专家知识)划分进行分区,然后使用地理探测器观察每个因子的得分。
Determinants’ Spectrum, Evolution
上面讲因子谱随空间变化,这里讲的是因子谱随时间的变化。可以算出 q-value 随时间的变化的曲线,然后得出一些结论。
Determinants’ Spectrum, btw modules
根据因子谱随着其它维度的变化讲故事。如,用同样的因子去解释三个目标变量。
S7. General Interaction
有一些因子,观察每个因子的 q-value 和它们两两交互情况下的 q-value 。
且地理探测器探究的是非线性作用,所以多个交互因子的得分加起来并不要求等于一,可能超过一。
Spatial Goodness of Fit
提出某个模型的性能较前人的模型有较大的提升,在分层异质性上做敏感性检验,可以用前人模型得出的结果放进地理探测器计算 q-value ,然后对比自己提出的模型计算出的结果丢进地理探测器计算出的 q-value ,算是一种量化指标。
GeoDetector+
地理探测器可以结合其它方法,如结合机器学习。
# 地理探测器特性
这里讲地理探测器的九个特性。
Nonlinear, even non-monotonic
地理探测器一大特性是非线性、非单调、可解释。
General Interaction
地理探测器可以做广义交互,不限于计量经济学的乘性交互。
Optimal Stratification
现有统计学不擅长做类型量(分类变量、离散型变量),现代统计学比较擅长连续型变量,虽然借助哑变量能起到一定效果,但如果样本量不多的话这几个哑变量很容易产生共线性,导致结果不可信。
地理探测器一大特性是适合对类型量进行估算。针对连续型变量,则需要将它们变为类型量后再用地理探测器进行计算。有以下几种办法可以将连续型变量转为离散型变量。
1.使用业内公认指标对数值进行分层
如根据联合国对贫困、富裕等的定义,结合人均GDP进行分层。
2.若业内没有公认指标,则使用自然间断点分级法分5~7层
人脑一般适合处理5~7层,这也是 ArcGIS 的默认分层数。
3.若5~7层时 q-value 还是不显著,则调整不同分层,直到结果满意
当调参侠。别人问那就是最小二乘法不也这样吗?啊对对对。
To get high q: De-trend by regression, then get q
若想得到可解释且比较高的 q-value ,且已经直到某种趋势的话。可以先用回归去趋势之后再用地理探测器计算 q-value 。
De-confounding: find SSH, then modelling in strata
去混杂。只用空间单元作为数据输入,则空间单元里很多是混杂的。应该凭地理规律分层,某个层内地理规律是一样的,分完层再modelling,这就是去混杂。
De-bias: find SSH
克服样本偏性。样本的直方图不等于总体的直方图,那么可以说样本有偏。总体存在分异性,样本没有覆盖所有的总体的层,那么样本的直方图就不会等于总体的直方图。如果不存在分异性,那么就不会存在样本的偏性。为了克服样本的偏性,首先需要检验样本是否有偏,那么就是检验总体是否分层,再看样本是否在所有层都覆盖了,如果都覆盖了那么就是数据无偏。
Direction: No due to non-monotonic; SSH then OLS in strata
方向性?没有方向,是非线性非单调关系。先分层,再用线性回归等方法把方向做出来。
Collinearity: immune
地理探测器对共线性免疫。
Visualization: updating
有更多的可视化办法把地理探测器结果给展示出来。
# 要点
地理探测器的 分层 使得建立的模型既能反应全局的规律也能揭露局部的特性。
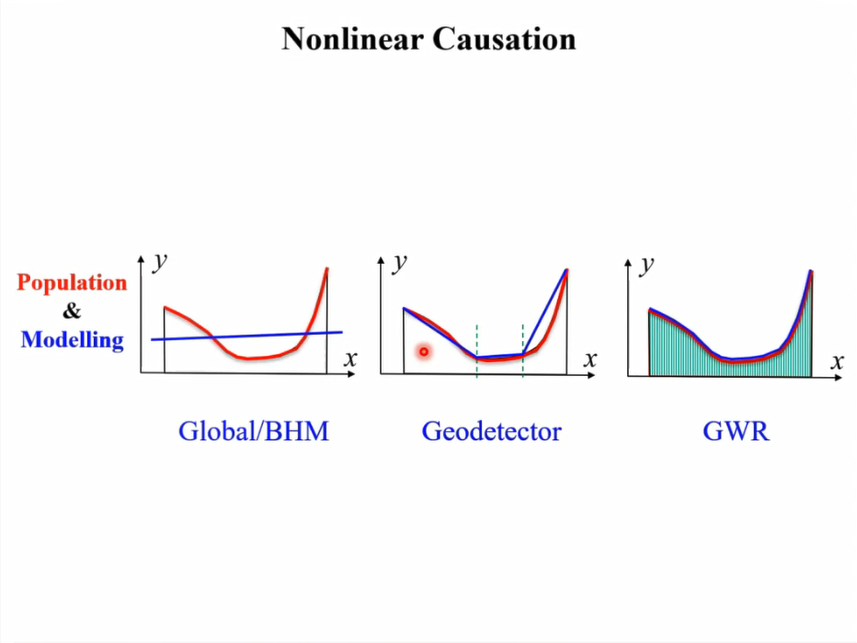
分层在自然界中也是相当普遍的事。
# 结果解释
使用 Excel 版的地理探测器计算 q-value 后会得到额外的四张表,分别是交互探测器、生态探测器、因子探测器和风险探测器。
交互探测器
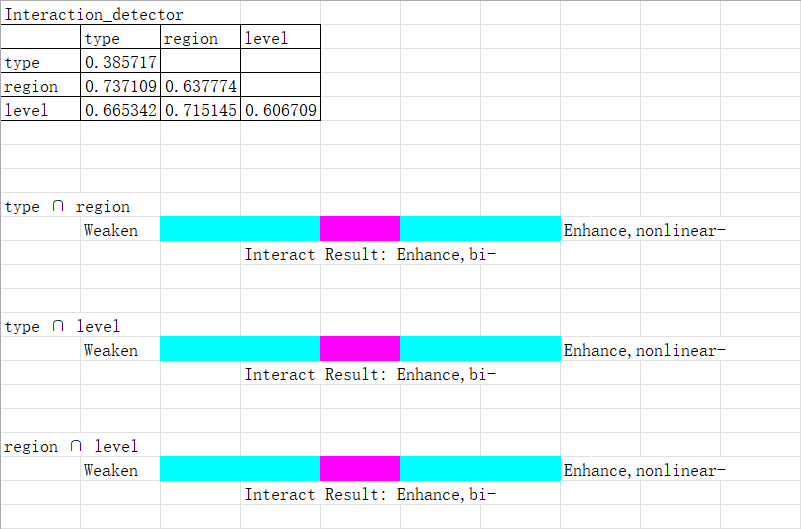
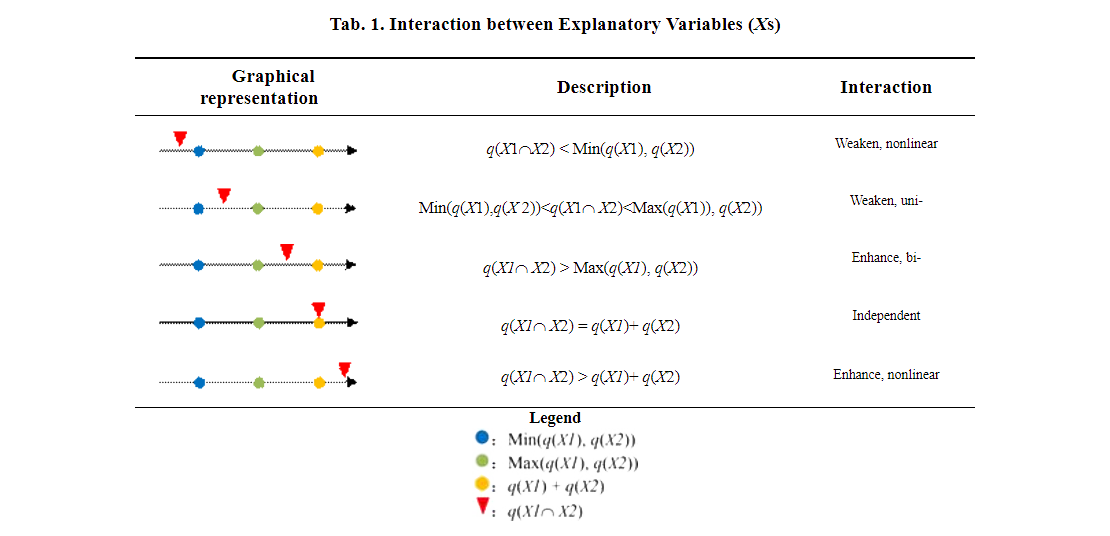
这里显示的是两两变量交互后的 q-value 。如单个变量type对发病率能解释38.5717%。但region和type的交互项能解释发病率的73.7109%。下面的图示表示交互后和交互前的关系,粉色块有五种可能的位置,从左往右代表非线性关系增强。(结果是Enhance, bi-)。
生态探测器
这里的生态来自流行病学。不是地理的生态。如果通过显著性水平为0.05的 F检验 ,则认为变量A对目标变量的解释力与变量B对目标变量的解释力有显著差异。可以通过结果看到,type对发病率的解释力与region对发病率的解释力有显著差异;type对发病率的解释力与level对发病率的解释力有显著差异;region对发病率的解释力与level对发病率的解释力没有显著差异。
| type | region | level | |
|---|---|---|---|
| type | |||
| region | Y | ||
| level | Y | N |
因子探测器
这里显示输入变量对目标变量的解释力。Type能解释发病率的38.5717%,p值为0.363236没有通过显著性检验;region能解释发病率的63.7774%,p值为0.000通过显著性检验;level能解释发病率的60.6709%,p值为0.04通过显著性检验。
q-value的一个简单变换满足非中心F分布
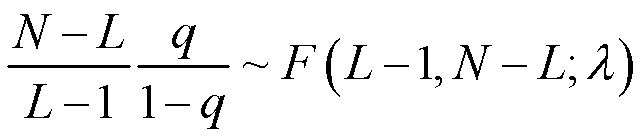
| type | region | level | |
|---|---|---|---|
| q statistic | 0.385717 | 0.637774 | 0.606709 |
| p value | 0.363236 | 0.000 | 0.040804 |
风险探测器
每个输入变量会有两个表格。第一个表格内容是每个变量的每个分类所对应的目标变量的算术平均值。第二个表格是该变量每两个分类的目标变量算术平均值是否有显著差异,用的是T检验。