coding_machine_learning。
# 序
通过之前课程的学习,知晓了机器学习的一些基本概念。该帖记录吴恩达新机器学习课程的学习过程,作为之前帖子的补充,并附上 pytorch 及 tensorflow 的相关代码。
# 机器学习概述
概述之后补充,还是先看看基本术语吧家人们。
基本术语
(色泽=青绿; 根蒂=蜷缩; 敲声=浊响)
括号内是一条记录,诸多记录的集合称为一个数据集 data set 。在数据集中,每条记录是关于一个事件或对象的描述,称为一个示例 instance 或样本 sample 。反应事件或对象在某方面的表现或性质的事项(色泽、根蒂、敲声)称为属性 attribute 或特征 feature 。属性上的取值(青绿、蜷缩、浊响)称为属性值 attribute value 。属性张成的空间称为属性空间 attribute space 、样本空间 sample space 或输入空间。把每个属性作为一个坐标轴,张成一个描述某个对象的多维空间,那么每个示例都可以根据自己的属性值找到自己的位置。由于在这个多维空间中,每个点都对应一个坐标向量,因此把每个示例称为一个特征向量 feature vector 。
如果希望得到一个“判断是否是好瓜”的模型,还需要训练样本的结果信息,这个结果信息被称为标记 label ,下面括号中最后的“好瓜”便是标记。
((色泽=青绿; 根蒂=蜷缩; 敲声=浊响), 好瓜)
拥有了标记的示例被称为一个样例 example 。用(xi, yi)表示第i个样例。yi∈Y是示例xi的标记,Y是所有标记的集合,称作标记空间 label space 或输出空间。
从数据中学得模型的过程称学习 learning 或训练 training ,训练过程中使用的数据称为训练数据 training data ,其中每个样本被称为一个训练样本 training sample ,训练样本组成的集合称为训练集 training set 。训练样本可能有标记,也可能无标记。
Terminology
- Training Set :训练模型的数据称为训练集。
- Input Feature :小写的 x 称之为特征、输入特征、输入变量。如房间大小、房间楼层等。
- Target Variable :小写的 y 表示想要预测的目标变量或输出变量。如房间的价格。
- m : Total Number of Training Examples ,表示训练样本的总个数。
- n :表示特征的个数。
- (x, y) :表示单个训练样本。
- (x(i), y(i)) :用表示第i个训练样本。这里i指第i行。
- xj :第j个特征。
 :第i个训练样本(行)的所有特征的值,是一个行向量。上面的箭头也可以省略,依旧表示行向量。
:第i个训练样本(行)的所有特征的值,是一个行向量。上面的箭头也可以省略,依旧表示行向量。 :第i个训练样本的第j个特征的值。
:第i个训练样本的第j个特征的值。- ŷ :对目标变量的估计值。如果上面没有小帽子 y ,则指的是训练集中的实际真实值。
- Hypothesis :假设函数,将输入映射到输入的函数。
- Parameter :指模型的参数,也称系数或权重。是在训练模型的过程中调整以改进模型的变量。
- Error :误差。预测值与真实值的偏差。
- Cost Function :代价函数。度量模型的总体误差,能够衡量算法的表现。可以带惩罚项(正则化项)。
- LOSS :指单个样本的损失。
- Objective Function :目标函数,一般来说要最小化目标函数。代价函数是目标函数的一类。只要定义一个代价函数为目标函数,它们则为同一个东西。
 :参数向量,等于 [w1,w2,…,wn] ,是一个行向量。
:参数向量,等于 [w1,w2,…,wn] ,是一个行向量。 :特征向量,等于 [x1,x2,…,xn] ,是一个行向量。
:特征向量,等于 [x1,x2,…,xn] ,是一个行向量。
来自线性代数的惯例,大写字母代表矩阵; 小写字母代表向量或标量。
# 线性回归
线性回归是机器学习中最简单的算法,在课程中也是第一个讲解的算法。课程由浅入深,先从单变量线性回归讲起,然后讲向量化,直到多变量线性回归。
单变量线性回归
单变量线性回归也称为 Univariate Linear Regression ,也就是输入特征只有一个的线性回归。
假设函数的标记
至于单变量线性回归的假设函数,可以写成 fw,b(x)=wx+b 。但大部分时候可以简写成 f(x)=wx+b 。
至于多变量线性回归的假设函数,根据上面的记号,可以写下图所示的公式。需要注意的是,里面是向量的点积,不是矩阵相乘(它们是向量不是矩阵)。那么这里的单变量到多变量线性回归是怎么来的呢?这里就要提到向量化了。
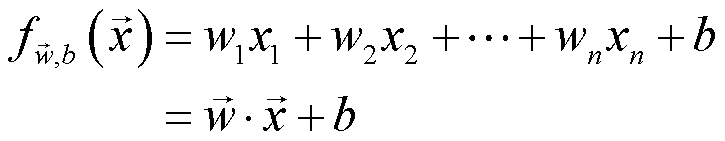
向量化
使用向量化不仅能让代码变短还能提高效率。使用 Numpy 的函数做线性代数计算还可以运用到Graphics Processing Unit,能够加速机器学习工作。
w_vector = numpy.array([1.1, 2.2, 3.3])
x_vector = numpy.array([10, 20, 30])
b = 1
# Hypothesis
f = numpy.dot(w_vector, x_vector) + bnumpy.matrix 是绝对二维的,而 numpy.ndarray 是n维度的。前者是后者的子集,所以前者继承了后者的所有属性和方法。补充:numpy的矩阵和n维数组
定义 numpy.ndarray 的时候最好定义清楚一点。
# 创建一个shape为(1, 5)的二维数组
vct1 = numpy.array([[1, 2, 3, 4, 5]])
vct1 = numpy.array([1, 2 ,3 ,4, 5]).reshape(1, 5)
vct1 = numpy.zeros((1, 5))
# 创建一个shape为(2, 3)的二维数组
vct2 = numpy.array([[1, 2, 3], [4, 5, 6]])
vct2 = numpy.array([1, 2, 3, 4 ,5, 6]).reshape(2, 3)
vct2 = numpy.zeros((2, 3))
# 创建一个shape为(3, 1)的二维数组
vct3 = numpy.zeros((3, 1))
vct3 = numpy.zeros(3).reshape(3, 1)
vct3 = numpy.array([[1], [2], [3]])
# 创建一个shape为(2, 3, 5)的三维数组
arr3 = numpy.zeros((2,3,5))
上面都定义的二维数组或三维数组,而向量是一维数组。
矩阵像下面定义。
# 创建1×3的矩阵,mat1.shape是(1, 3)
mat1 = numpy.matrix([1, 2, 3])
# 创建2×5的矩阵,mat2.shape=是(2, 5)
mat2 = numpy.matrix([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
# 创建一个1×3的矩阵
mat1 = numpy.matrix(numpy.zeros(3))
mat1 = numpy.matrix(numpy.zeros((1, 3)))
# 创建一个3×1的矩阵
mat3 = numpy.matrix(numpy.zeros((3, 1)))
mat3 = numpy.matrix(numpy.zeros(3)).T
mat3 = numpy.matrix(numpy.array([[1], [2], [3]]))
一维数组是没办法进行转置的。如 numpy.zeros(3) 创建的是一维数组,如果要转置,需要先把它转为矩阵或更改为多维。
# 创建一维数组,此时是无法进行转置的
vct = numpy.zeros(3)
# 更改维度为(1, 3),这是二维
vct.shape = (1, w.shape[0]) # 或创建时写成 vct = numpy.zeros((1, 3)) 或创建时写成vct = numpy.zeros(3).reshape(1, 3)
# 或转为矩阵
# vct = numpy.matrix(vct)
# 转置
vct = vct.T多变量线性回归
课程中的单变量线性回归主要用来引入,重点还是多变量线性回归。下面讲多变量线性回归。学习率也放在下面讲。
Squared Error Cost Function
平方误差代价函数是机器学习中的线性回归模型中最简单也是最常用的代价函数。它通过计算每个预测值与真实值的距离平方之和的均值来度量该学习算法性能的好坏。
平方误差代价函数(多变量线性回归)
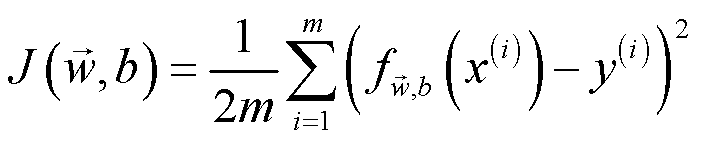
实际上这个平方误差代价函数是一个Convex Function,特性之一是有一个全局最小值。代价函数度量算法性能的好坏,代价函数的值越小,学习算法性能越好,我们需要一个 方法 来获取算法的参数来使得代价函数值最小。
这个方法就是 梯度下降 。梯度下降能根据代价函数的偏导数,同时迭代更新每个参数的值,使得代价函数达到最小后停止。
注:负梯度指明了梯度下降的方向,使得损失函数降低。
多变量线性回归梯度下降
上面给出了向量化方式实现的多变量线性回归平方误差代价函数。接下来运用梯度下降调整每个参数以获得最小的损失。
多变量线性回归梯度下降
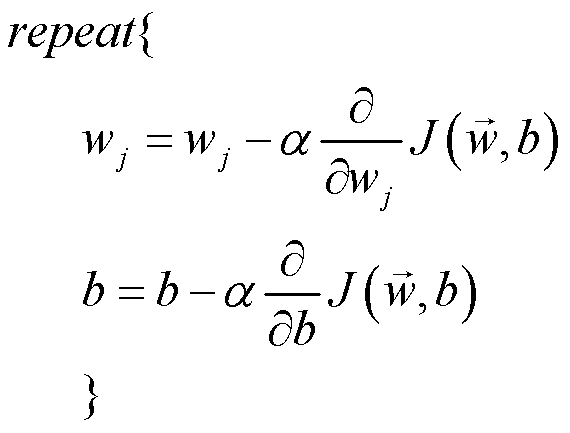
将代价函数的偏导项求解出,来再带入上图中的公式,得:
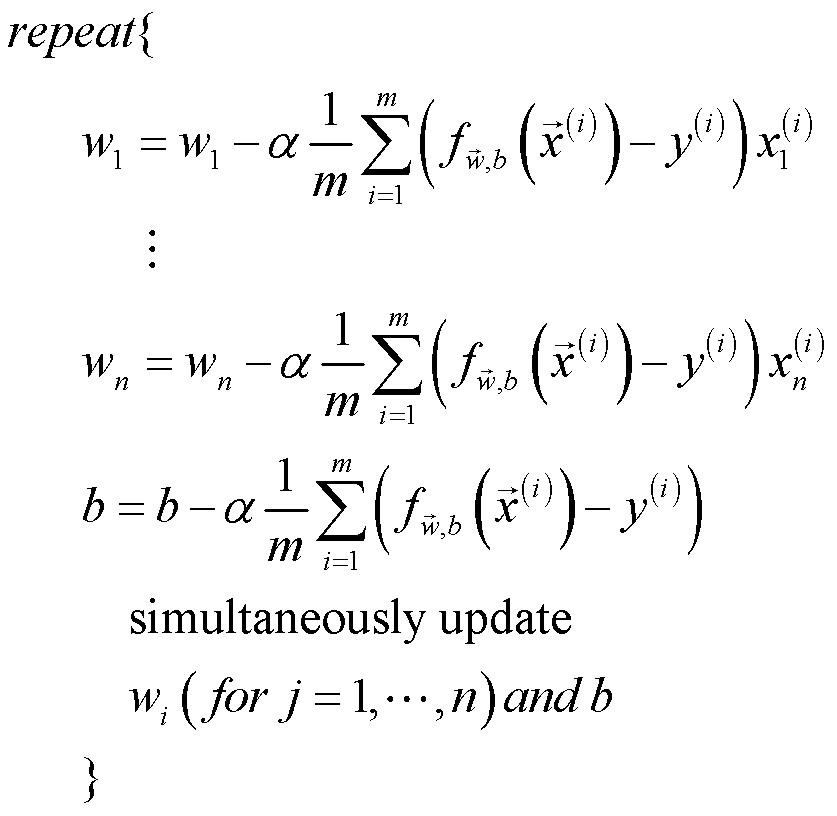
多变量线性回归梯度下降代码实现
Learning Rate
可以看到梯度下降里有一个希腊字母 α ,这是梯度下降中的学习率。学习率是机器学习的超参数,控制每一次梯度下降迭代的步长。
学习率如果设置过大,则算法无法收敛(发散);如果设置太小,则会花较多时间收敛。因此学习率的设置会影响算法的性能。
hyperparameter
超参数,是在开始学习过程之前设置值的参数。 相反,其他参数的值通过训练得出。
正规方程
在多变量线性回归的参数求解中, Normal Equation 也不失为一种方法。基于正规方程的线性回归参数求解思想也是让平方误差代价函数为最小值。上文讲到过,平方误差代价函数是一个Convex Function,存在全局最小值。这个全局最小值恰好在代价函数对参数 W 求偏导为0的时候出现。
为了实现上述目标,就需要先把参数都向量化(包括截距项b,作为w0放到参数向量中)。并把所有的特征做成矩阵。让平方误差代价函数用矩阵来表示。
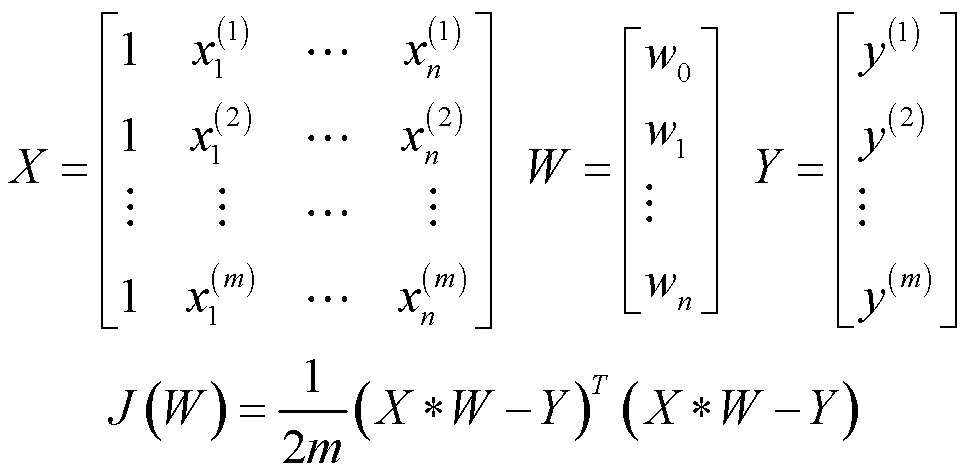
将平方误差代价函数化简后,对 W 求偏导。令该值等于0,然后解方程:
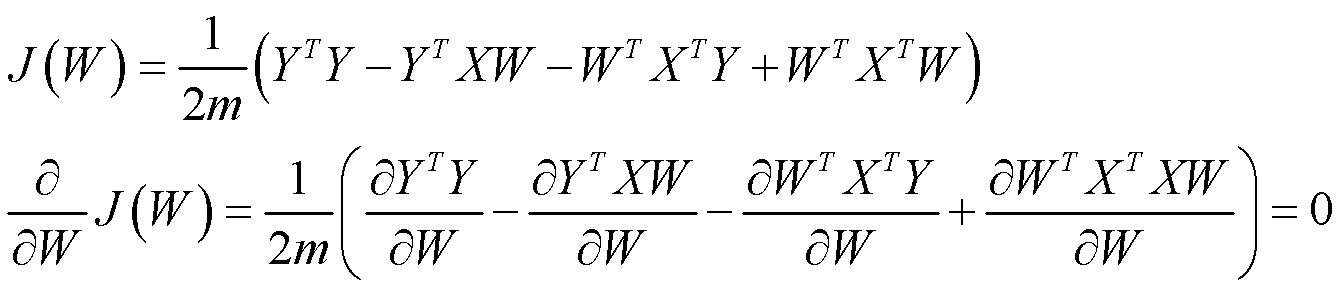
偏导数第一项为 0 ;第二项为 XTY ;第三项为 XTY ;第四项为 2XTXW 。因此得 (1/2m)*(-2XTY+2XTXW)=0 。最后得到:
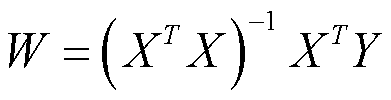
在Numpy中
*乘是矩阵对应位置的点乘得到的还是矩阵;点乘是内积
多项式拟合
将多项式回归和特征工程的思想结合起来,运用到多项式回归中,来拟合出曲线。通过特征工程可以创造出很多高次项多项式,将新的特征放进多项式回归中,会为每一个特征计算出参数。随着梯度下降的运行,有些特征的参数会一直减小直到零或非常接近零,说明这个特征是没用的。
在进行多项式拟合时, 特征缩放 是非常重要的,因为特征工程创造出的新特征和原特征的范围相差可能会很大。为了最终参数能够比较,在进行多项式拟合之前做一个 特征缩放 是必要的。
多项式回归梯度下降代码实现
# Numpy中的各种乘法
在 Numpy 中的矩阵虽然是N维数组的子集,但各种乘法或 * 运用在它们身上可能表达不同的意思。该点非常重要,因为在编程中可能用到各式各样的数据对象和计算。
numpy.dot()
首先把目光放到最复杂的 dot() 方法。
# 数组与标量
numpy.dot(arr1, scalar) # 标量作用于每一个元素上
# 一维数组与一维数组
numpy.dot(arr1, arr2) # 向量内积,返回一个标量
# m×n的矩阵与n×m的矩阵
numpy.dot(mat1, mat2) # 矩阵乘法
# m×n的矩阵与n×m的二维数组
numpy.dot(mat1, arr1) # 矩阵乘法
numpy.multiply()
# 数组与标量
numpy.multiply(arr1, scalar) # 标量作用于每个元素上
# m×n的矩阵与m×n的矩阵(或数组)
numpy.multiply(mat1, mat1) # 对应元素点乘,返回一个m×n的矩阵
# m×n的矩阵与m×1的矩阵或二维数组
numpy.multiply(mat1, arr1) # 前者每一列对应元素都会与后者对应元素点乘,返回m×n的矩阵
# m×n的矩阵与1×n的矩阵或二维数组
numpy.multiply(mat1, arr1) # 前者每一行对应元素都会与后者对应元素点乘,返回m×n的矩阵
# m×1的数组与1×n的数组,或n个元素的一维数组与m×1的二维数组或矩阵
numpy.multiply(arr1, arr2) # 返回m×n的数组
# shape一致的一维数组与一维数组,和*的结果一致
arr1 * arr2 # 对应元素相乘,返回shape一致的一维数组
# n个元素的一维数组与m×n矩阵(或二维数组)
numpy.multiply(arr1, mat1) # 一维数组的每个元素都与矩阵每一行的每个对应元素相乘,返回m×n矩阵
numpy.matmul()
# 矩阵与矩阵或数组,该方法不支持标量乘法
numpy.multiply(mat1, arr1) # 矩阵乘法,返回矩阵*
# 标量与数组或矩阵
arr1 * 2 # 标量作用于每个元素上
# m×n矩阵与n×b矩阵或二维数组。必须有一个是矩阵才行,两个都是二维数组是会出错的。
mat1 * mat2 # 矩阵乘法,返回m×b矩阵
# shape一致的一维数组与一维数组
arr1 * arr2 # 对应元素相乘,返回shape一致的一维数组# 特征缩放
不同特征的值的区间范围可能有很大差别,更不用说多项式会使得区间更大,然而不同特征若取值范围相差过大,在梯度下降时可能会来回弹跳很长一段时间,才能最终找到全局最小值。所以需要 特征缩放 ,使得不同特征的取值范围有可比性,进而提升梯度下降性能。
特征缩放 只运用于输入特征X,不运用于目标变量。
且想要良好运行梯度下降,要保证各特征的取值范围不要相差太大,太大太小都是不行的。如[0, 3],[-2, 0.5],[-1, 1],[-3, 3],[-0.3, 0.3]都是可以的。但[-100, 100]就太大了,[-0.001, 0.001]又太小了。
除以最大值
300≤x1≤2000
0≤x2≤5
除以最大值的特征缩放方法就是除以该特征的最大取值,如x1就可以缩放为 0.15≤x1,scaled≤1 ,x2可以缩放为 0≤x2,scaled≤1 。
Mean Normalization
Mean Normalization 可以将特征的值缩放到 [-1, 1] 。均值归一化公式如下: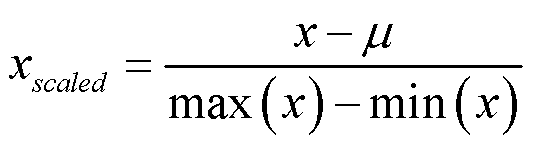
Z-Score Normalization
该方法的公式是 xscaled=(x-μ)/σ ,其中 μ 是该特征的均值, σ 是该特征的标准差。
# get biased estimates with sk-learn
from sklearn import preprocessing
scaler = preprocessing.StandardScaler()
scaled_v = scaler.fit_transform(data.loc[:, ['Size']])
# get unbiased estimates with numpy
data.loc[:, 'Size'] = (data.loc[:, 'Size'] - data.loc[:, 'Size'].mean()) / data.loc[:, 'Size'].std()# 分类器
在线性回归里目标变量是连续型变量,可以为任意数值。但在本章,目标变量是哑变量,仅有有限个数的结果,可以看作是分类问题。由于线性回归无法很好处理分类问题,这里由二分类Logistic回归引入,介绍SVM、RF、NN等一系列分类算法。
对于二分类问题,要根据问题的本身来确定 negative class 和 positive class 分别指代什么,前者也可称为反例(False或0),后者可称为正例(True或1)。如一个判断邮件是否为垃圾邮件的问题,则正例是垃圾邮件,反例不是垃圾邮件。
Decision Boundary
在介绍分类器之前提一下决策边界,结合具体的某个分类器来理解决策边界更容易。在使用分类器时我们需要一个阈值,高于该阈值分类器输出一个结果,低于该阈值分类器输出另一个结果。
假如阈值为0.5,分类器在决策边界上的输出值应为0.5(中立),对于下图的 Logistic Regression 而言,若想 g(z) 为0.5,那么里面的 z 就需要为0(根据函数的图像)。
下图将线性决策边界可视化,方便理解。非线性决策边界和多项式回归类似,加入高次项实现。如果只使用 x1,..xn 而不包含高次项,则决策边界永远是线性的。
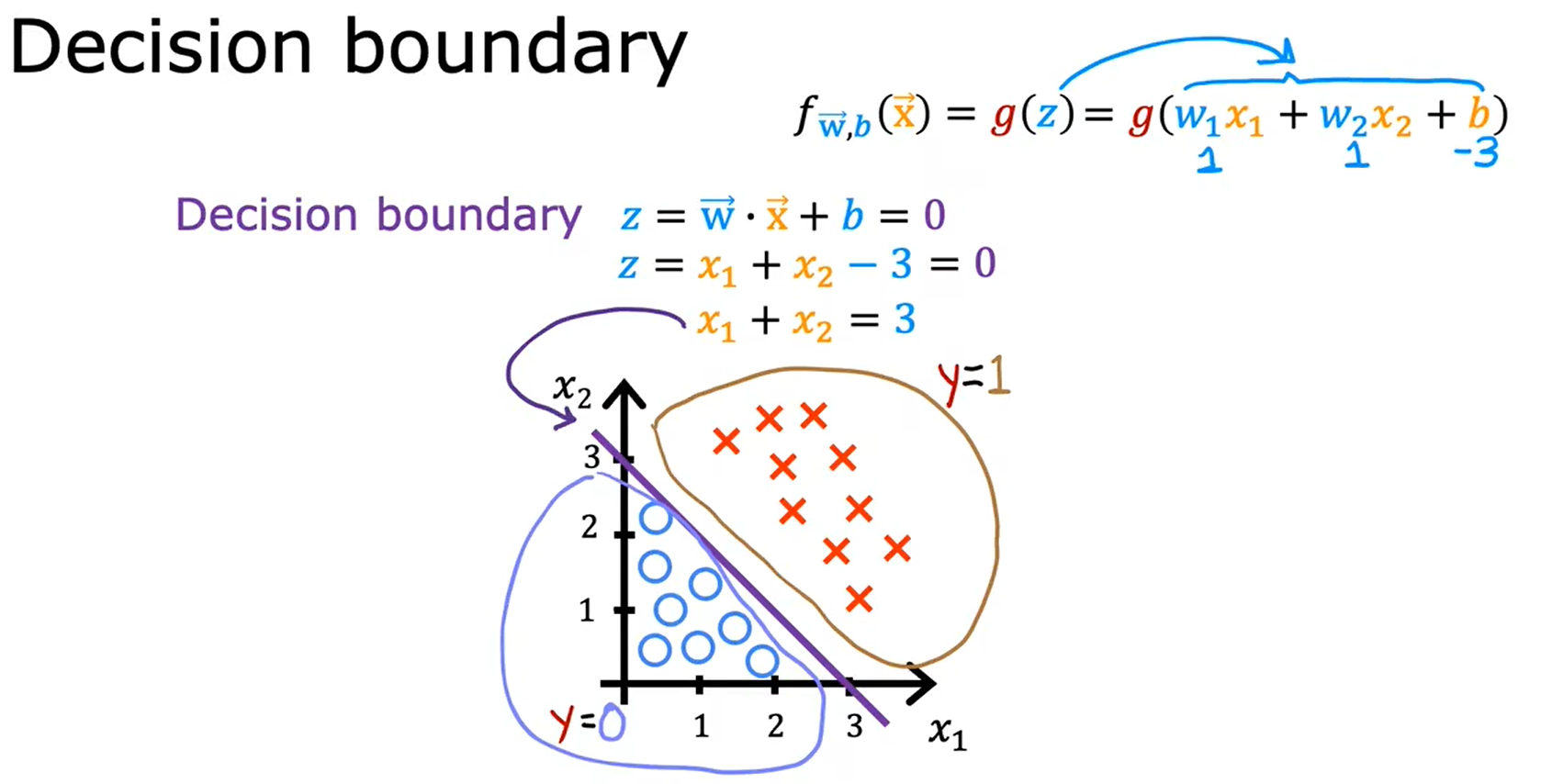
Logistic Regression
在 Logistic Regression 中有一个非常重要的函数,叫做 sigmoid function 。具体公式如下所示:
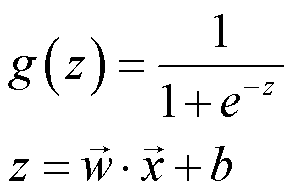
那么 Logistic Regression 的模型可以写为:
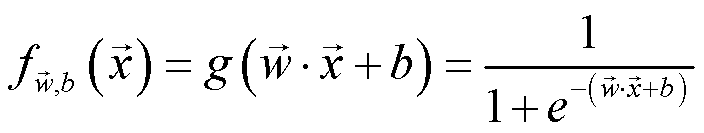
该模型只返回 (0, 1) 之间的数字。这个数字的意义为,得到标签为1的概率。如在垃圾邮件判别问题中得到0.7,则模型认为该邮件是垃圾邮件的概率为70%。所以模型也可以写成:
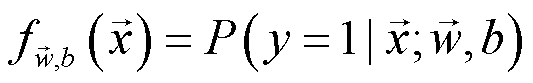
LOSS
平方误差代价函数作为该分类器的代价函数效果并不理想,带入公式中是一个 non-convex function ,存在局部最优解,而非全局最优解。因此需要另一个代价函数来使代价函数变为凸函数。
设 L 为单个训练样本的损失函数,则有:
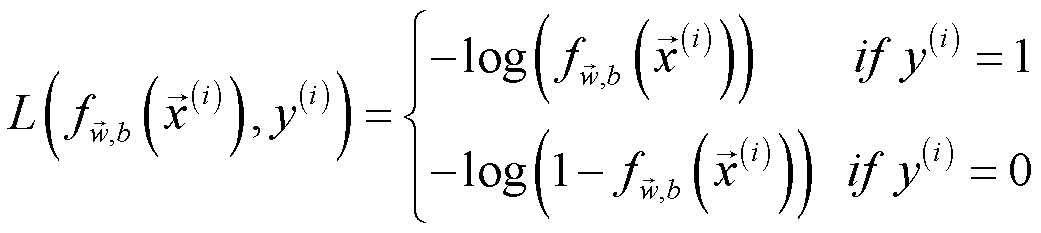
根据该函数的图像,分类器得出的预测值与目标变量的差异越大,损失就会越大。该代价函数可以简化为:
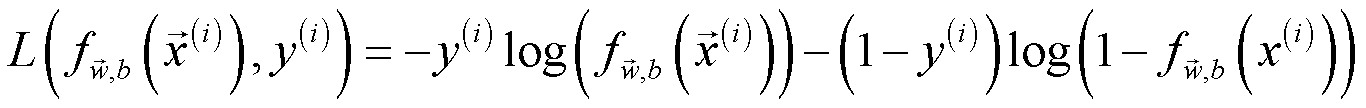
该代价函数的思想来自最大似然估计。
梯度下降
上一节展示了单个训练样本的损失函数 L ,那么所有样本的损失函数为:
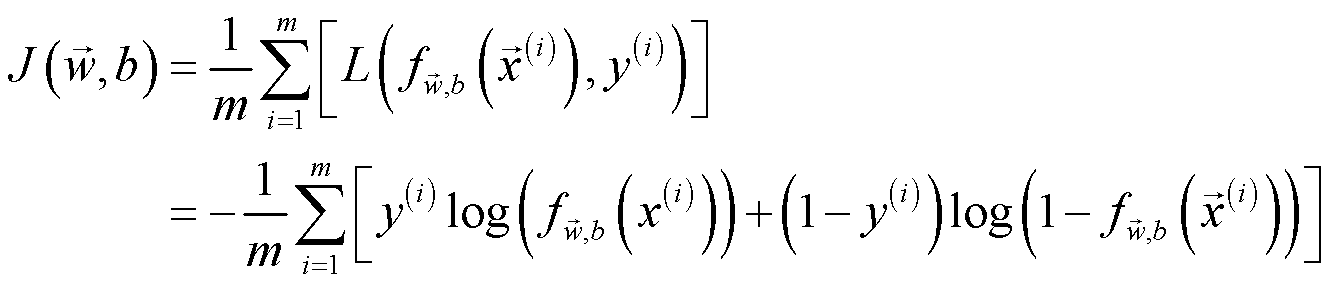
再根据梯度下降的思想,同步更新所有参数:
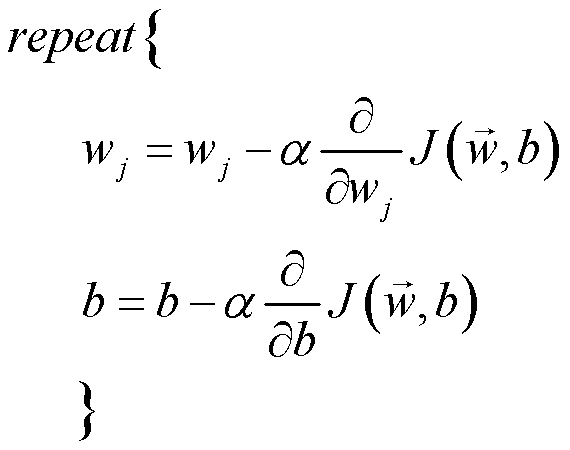
里面的偏导项为:
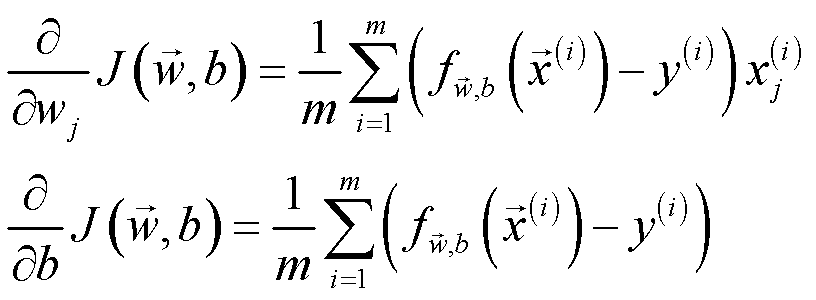
logistic回归梯度下降代码实现
# 正则化
使用不同的模型与特征进行回归分析,结果将有以下三种:
欠拟合-Underfit
High bias,模型本身的偏见导致的拟合不佳、偏差较大的情况。过少的特征将导致这一问题。
刚好-Just right
既拟合得好又具备泛化能力。
过拟合-Overfit
High variance,拟合得过于好以至于缺乏泛化能力。过多的特征将导致这一问题。
解决过拟合问题
有3种方法解决过拟合问题:
- 收集更多数据。
- 使用更少的特征,如减少高次项特征或其他特征,后者意味损失一部分与目标变量有关的信息。
- 正则化。保留所有的特征,但把系数降到非常小,以避免其产生过大的影响。
正则化仅运用在减小系数的大小上,对截距项使用正则化没有什么意义。
实际上,正则化就是选取合适的 正则化参数-λ 以使得下图中的代价函数最小,也就是第一项和第二项之和最小。因为当 λ 取〇时,相当于没有正则化,该过拟合还是过拟合;当 λ 取无限大时,所有系数都会被惩罚到〇,只剩个截距项,变成欠拟合的情况(如下为正则化线性回归损失的计算公式)。
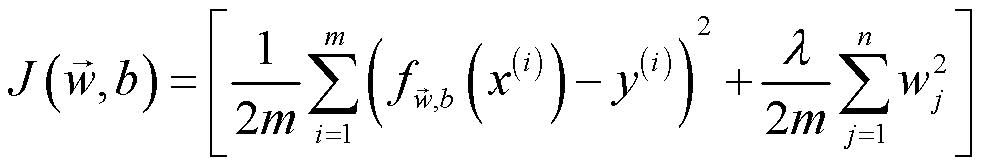
线性回归正则化
实际上,正则化项改变了线性回归的代价函数,进而改变了它的偏导数。因此梯度下降时的函数也发生了改变。
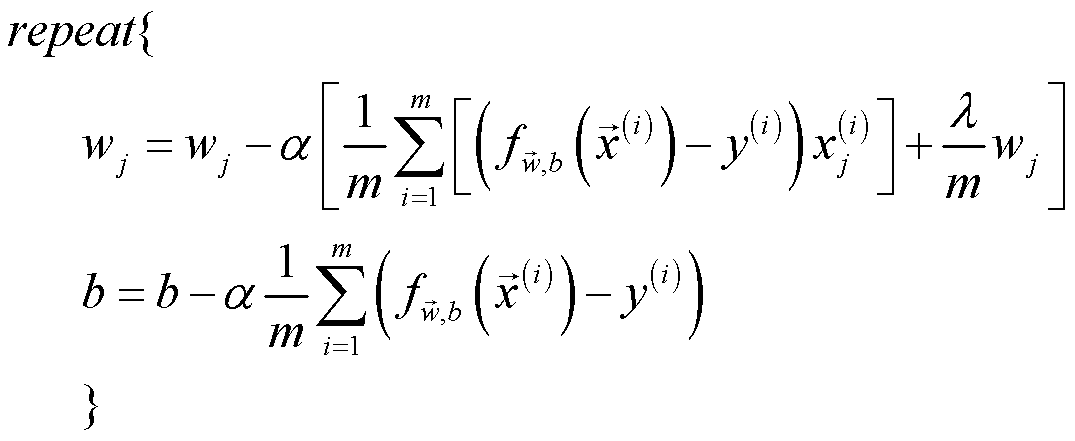
识别出这一点,就可以在 Python 中实现正则化线性回归梯度下降法求解了。
正则化线性回归梯度下降法代码实现
Logistic regression正则化
首先回顾一下 Logistic Regression 计算损失的数学公式:
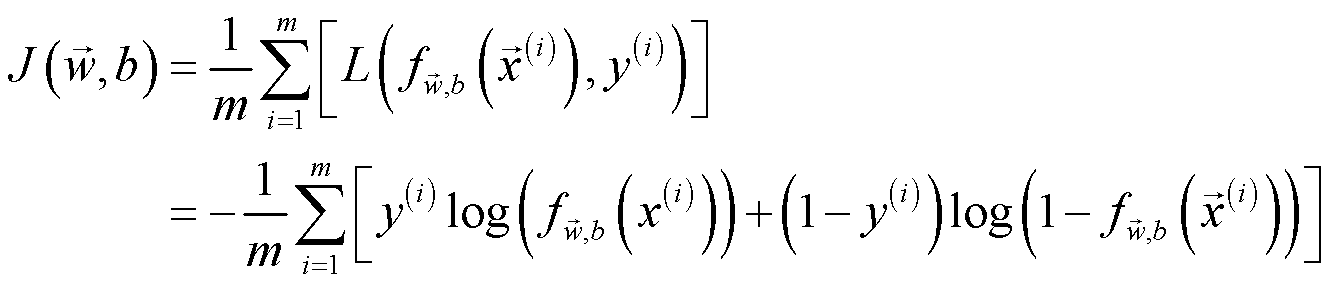
在末尾添加正则化项,得到正则化Logistic回归计算损失的数学公式:
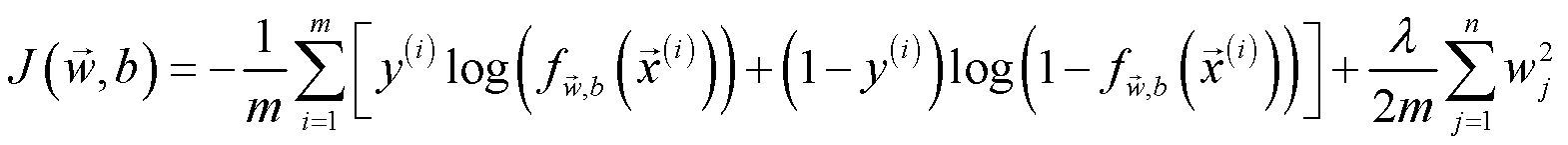
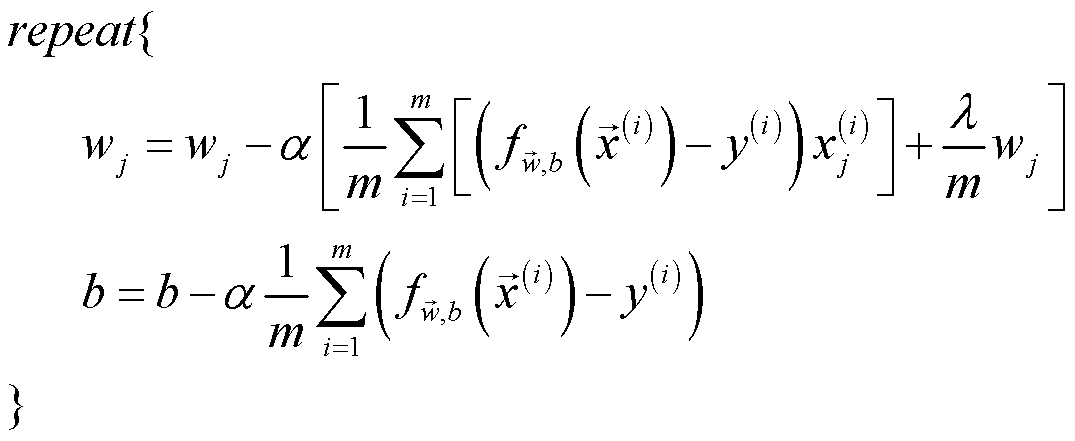
其中,正则化梯度的计算公式如下:
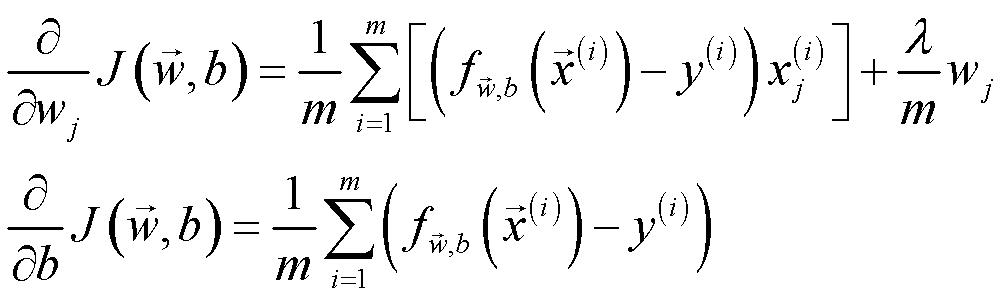
值得注意的是,正则化梯度的计算公式对 logistic regress 和 linear regression 来说是几乎一致的,唯一不同的是 fw,b(x(i)) ,前者为 fw,b(x(i))=g(z) ,而后者是 fw,b(x(i))=wx+b 。
剩余部分见此处。
# 神经网络
# 拟合后处理(通用)
# 机器学习算法开发步骤(通用)
# 偏斜数据集的误差指标(通用)
# 决策树