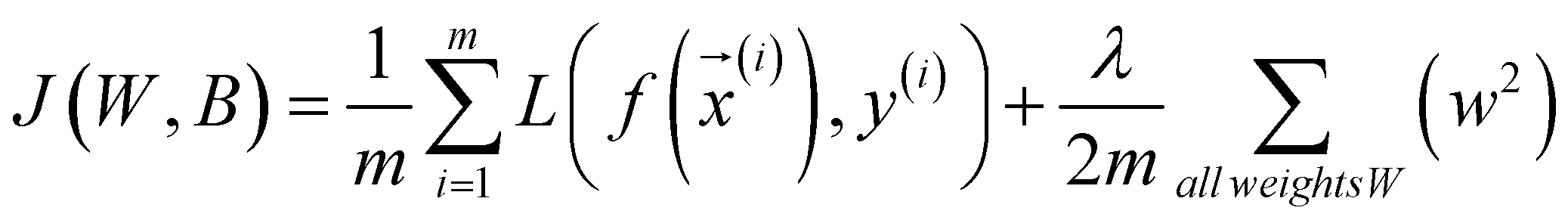紧接_1。
# 序
machine_learning_with_code帖子太长,改用新的帖子记录神经网络部分。
# 神经网络
使用他人训练得到的神经网络参数进行预测的行为被成为推理 Inference 。传统学习算法 Linear/Logistic Regression 无法利用数据量提升带来的优势,大量的数据并不会显著提升模型的表现/预测精度。而对于神经网络来说,越大型的神经网络它的表现/精度往往越好。因此在大数据时代神经网络得到较快的发展。
一个简单的神经网络架构 neural network architecture 如下图所示,可以发现完整的神经网络由输入层、隐藏层、输出层组成。将原始数据按层序输入隐藏层的每一个神经元,而后每层的神经元将向其后的层输入激活值(向量)。输出层依旧由神经元组成,在这里将进行最后的运算并输出最终结果。最后,神经网络也被称为 multilayer perceptron 。
越靠近输出层,隐藏层内的单元会越来越少。这是一种典型的神经网络架构。

值得注意的是,尽管传统的神经网络由诸多 logistic unit 组成,前者的性能远强于后者。神经网络能够基于特征向量学习自己的特征,而不是像后者一样需要人工特征工程。因此,在使用神经网络时需要做的决定之一是确定隐藏层及每层隐藏层所含神经元数量。值得注意的是,其他函数能够取代传统的 sigmoid function 。
Layers
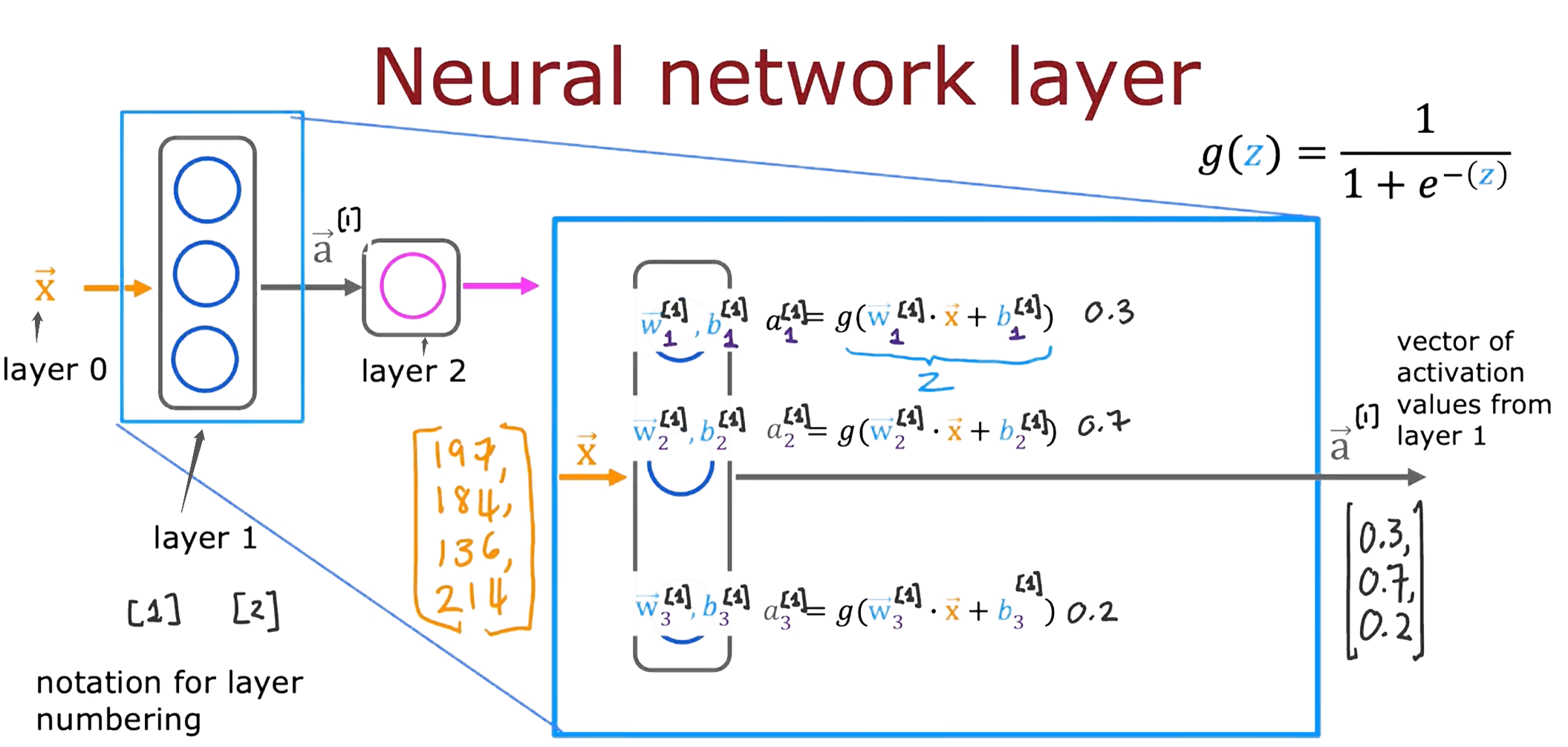
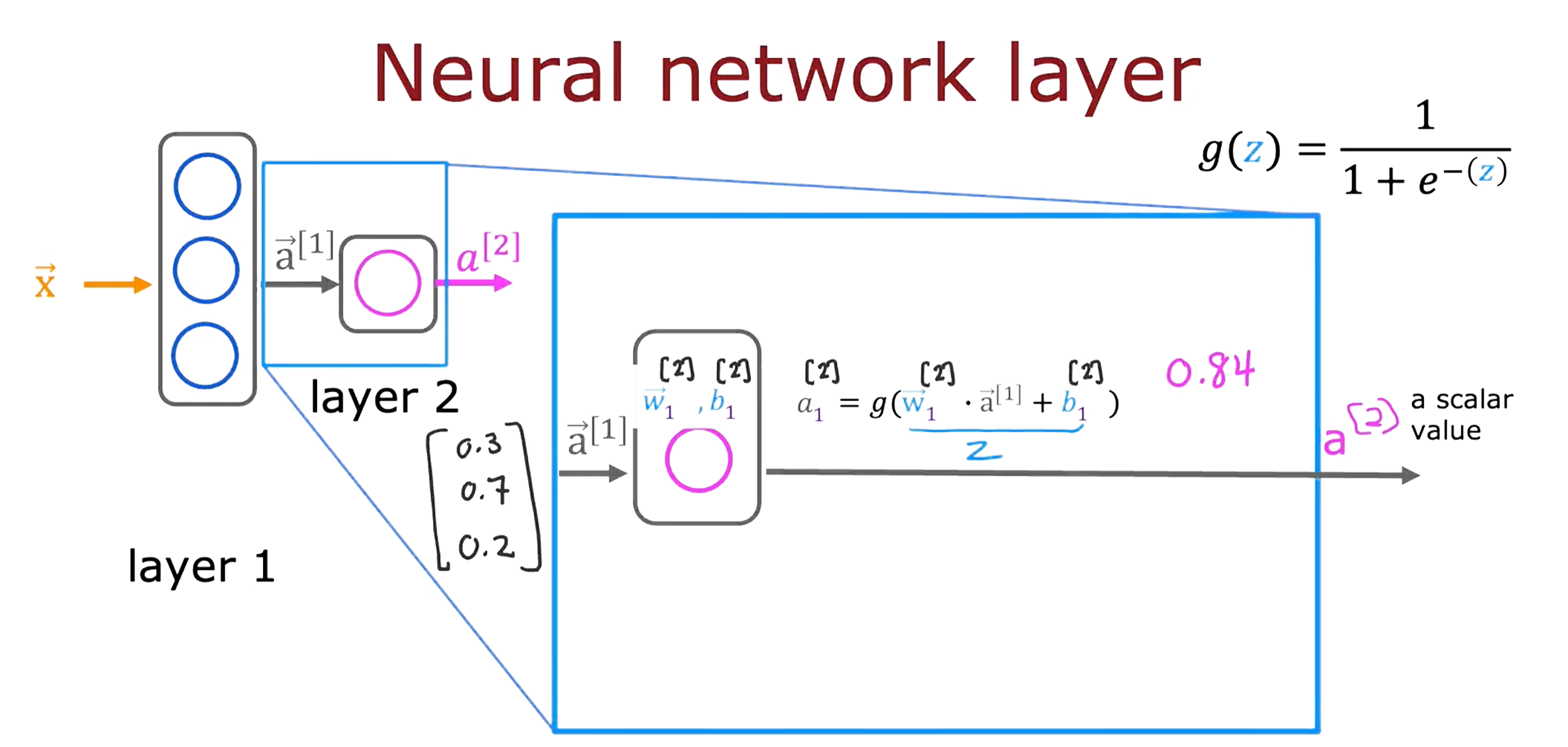
下图从层的角度展示神经网络从输入到输出的过程。下图所示的案例将特征向量(四个特征)输入第一层 layer 1 中的每一个神经元,并进行 lr 。然后将每一个神经元输出的激活值组成向量,输入至下一层的每一个神经元,并进行 lr 。最后一层仅有一个神经元,因此输出一个介于 0~1 的标量。需要注意的是,激活值 a 的下标代表输出该值的神经元于层中的次序,带有中括号的上标意味输出该值的神经元所在层的层序。
输入层为 layer 0 ,第一个隐藏层为 layer 1 …,以此类推。
复杂神经网络Notation
如下图所示的复杂神经网络,该架构共含4层,其中3层为隐藏层,第四层为输出层,计数时输入层 Layer 0 不被计入在内。第L层中第J个神经元的输出激活值也在下图中表示。为使符号一致,最初的输入向量可以被称为 a[0] 。最后一个输出标量的神经元 a[4] 可以被写为 f(x) ,这个标志也是之前线性回归等函数的输出的标志。
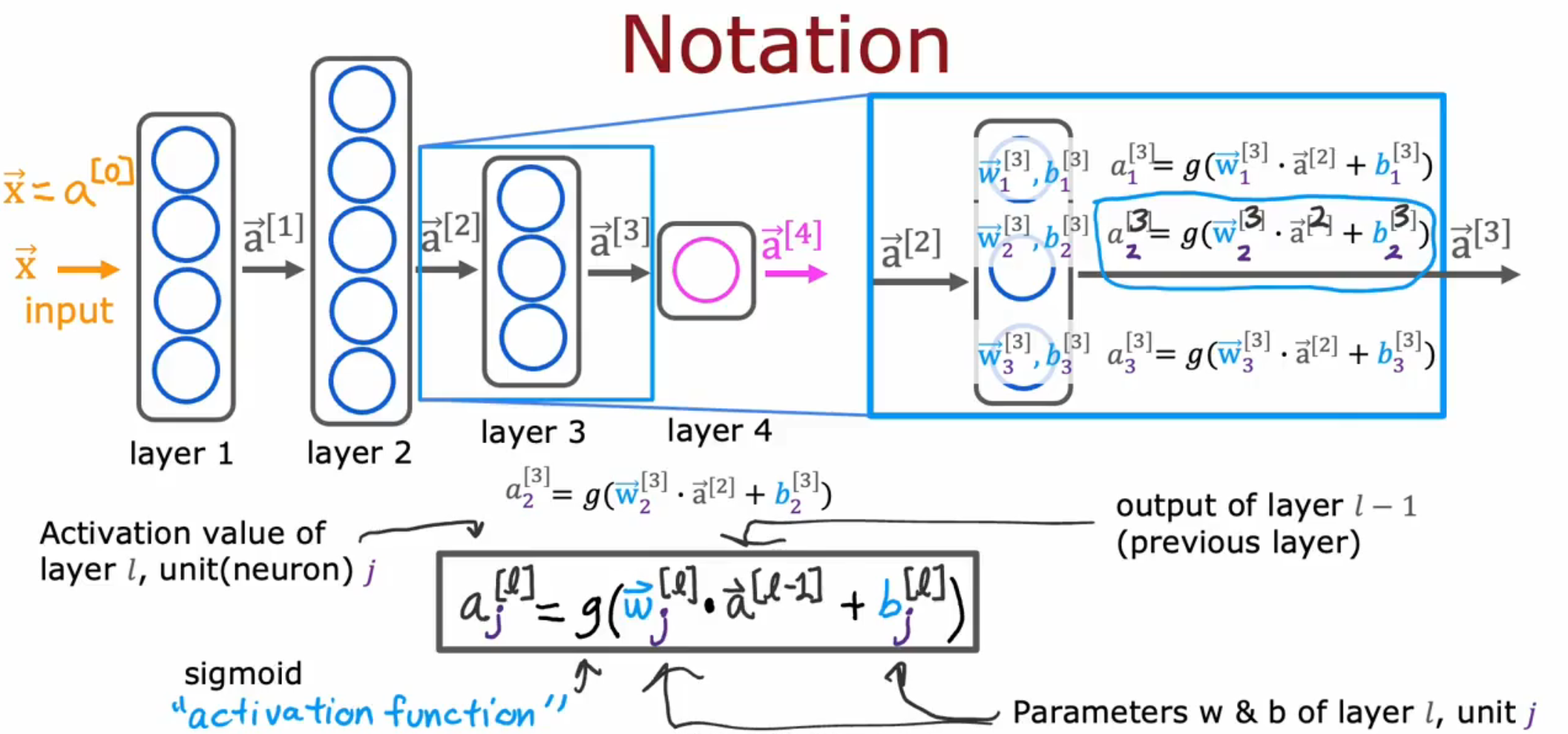
这种从左至右进行的计算也被成为向前传播 Forward Propagation ,因为整个计算过程在向前传播激活值向量,这与之后提到的反向传播 Backward Propagation 形成对比。
代码实现
以下为 TensorFlow 代码:
# 输入数据,看作是输入层
x = numpy.array([[200.0, 18.0]])
# 定义第一个隐藏层,内涵3个单元,激活函数为sigmoid函数
layer_1 = Dense(units=3, activation='sigmoid')
# 计算一个隐藏层的激活向量
a1 = layer_1(x)
# 创建输出层,内涵1个单元,激活函数同上
layer_2 = Dense(units=1, activation='sigmoid')
# 计算输出标量
a2 = layer_2(a1)
# 查看a1
a1 -> tf.Tensor([[0.2 0.7 0.3]], shape=(1, 3), dtype=float32)
# 将a1转为Numpy的多维数组
a1.numpy() -> array([[1.4661001, 1.125196, 3.2159438]], dtype=float32)
# 查看a2
a2 -> tf.Tensor([[0.8]], shape=(1, 1), dtype=float32)
# 将a2转为Numpy的多维数组
a2.numpy() -> array([[0.8]], dtype=float32)进一步观察变量 a1 ,它的数据类型是张量 tf.Tensor 。该数据类型旨在于图形卡上有效存储和执行矩阵计算。可以简单地把张量看作矩阵,虽然它不同于简单的矩阵。
ANI (Artificial Narrow Intelligence) & AGI (Artificial General Intelligence, 强人工智能):
AI分为ANI与AGI,ANI指应用于单个任务的AI,如医疗、工业、农业等; 而AGI指能够像真正人类做任何事的AI。相对于几十年来ANI取得巨大进展来讲,AGI取得的进展相对较少。研究人员通过模拟人脑以构建神经网络,然而实际上大脑的实际运作方式被了解地太少。如果有朝一日神经学取得突破进展,AGI可能也会因此受益。
矩阵乘法
矢量化(向量化)是神经网络如此高效的原因之一,因此学好并用好矩阵乘法至关重要。
# TensorFlow实现
基于 Sequential() 搭建一个神经网络:
import tensorflow
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
# 定义数据集、结果变量和迭代次数
X, y, iters
# 定义第一个隐藏层、第二个隐藏层和输出层
layer_1 = Dense(units=4, activation='sigmoid')
layer_2 = Dense(units=3, activation='sigmoid')
layer_3 = Dense(units=1, activation='sigmoid')
# 定义Sequential模型,注意层应依次填入
model = Sequential([layer_1, layer_2, layer_3])
# 编译并训练模型,编译时可指定损失函数。如在01两个数字识别的二元分类问题中,选择了二元交叉熵函数。回归问题可以选择MeanSquaredError()函数。
model.compile(...) # model.compile(loss=BinaryCrossentropy())
model.fit(X, y, epochs=iters)
# 预测、推理
model.predict(X_new)Sigmoid激活函数的替代方案
除了 sigmoid ,还有三个被广泛运用的激活函数: ReLU 、 Softmax 和线性激活函数 Linear activation function 。最后一个也被称为没有激活函数 No activation function 。
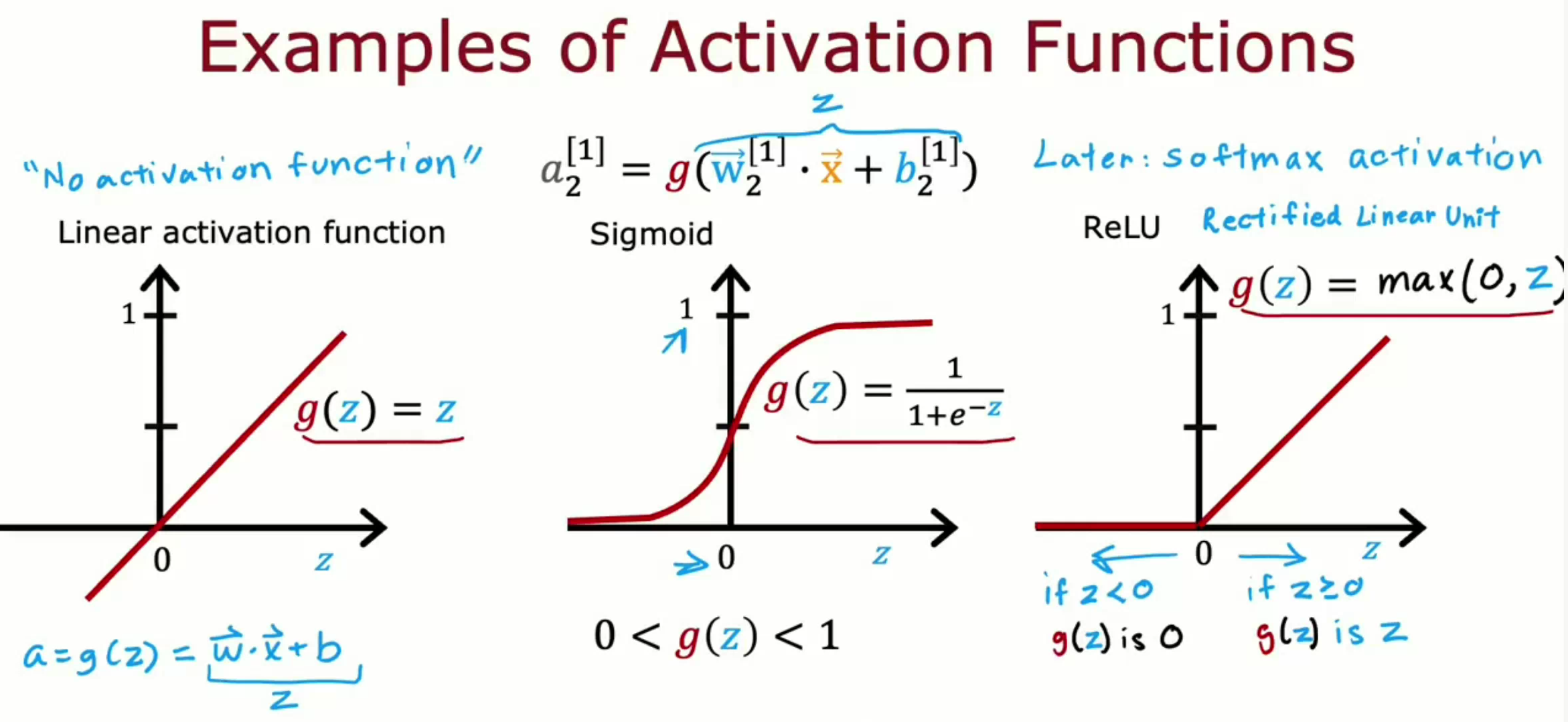
如何选择激活函数
神经网络中不同神经元可以采用不同激活函数。
关于 Output layer 的激活函数选择,应根据输出目标选择合适的激活函数:
- 01二元分类问题中目标变量为0或1,选择 sigmoid 函数。
- 回归问题中若目标变量既有负数也有正数和零,选择线性激活函数 Linear activation function 。
- 回归问题中若目标变量为0或>0的数,选择 ReLU 。
关于 Hidden layers 的激活函数选择,一般选择 ReLU 。因为它相比 sigmoid 而言在计算激活值与梯度时所消耗的计算资源更少。
from tf.keras.layers import Dense
model = Sequentials([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
# 若输出目标为01二元分类值,那么选择sigmoid
# 若输出目标为0或大于0的值,那么选择relu
# 若输出目标既有负数也有正数和零,那么选择linear
Dense(units=1, activation='sigmoid'),
])最后,如果所有神经元都采用线性激活函数,那么该神经网络将变得与普通线性回归没有什么不同; 若所有隐藏层都采用线性回归而输出层采用 sigmoid ,那么该神经网络将变得与普通LR别无二致。
多分类问题
多分类问题指的是识别目标的确切类型。使用 Softmax 处理多分类问题,如数字0123…9的识别等。下图描绘该激活函数在四分类问题下的激活值的计算公式:

下图显示的是该激活函数单条样本的损失值计算公式:
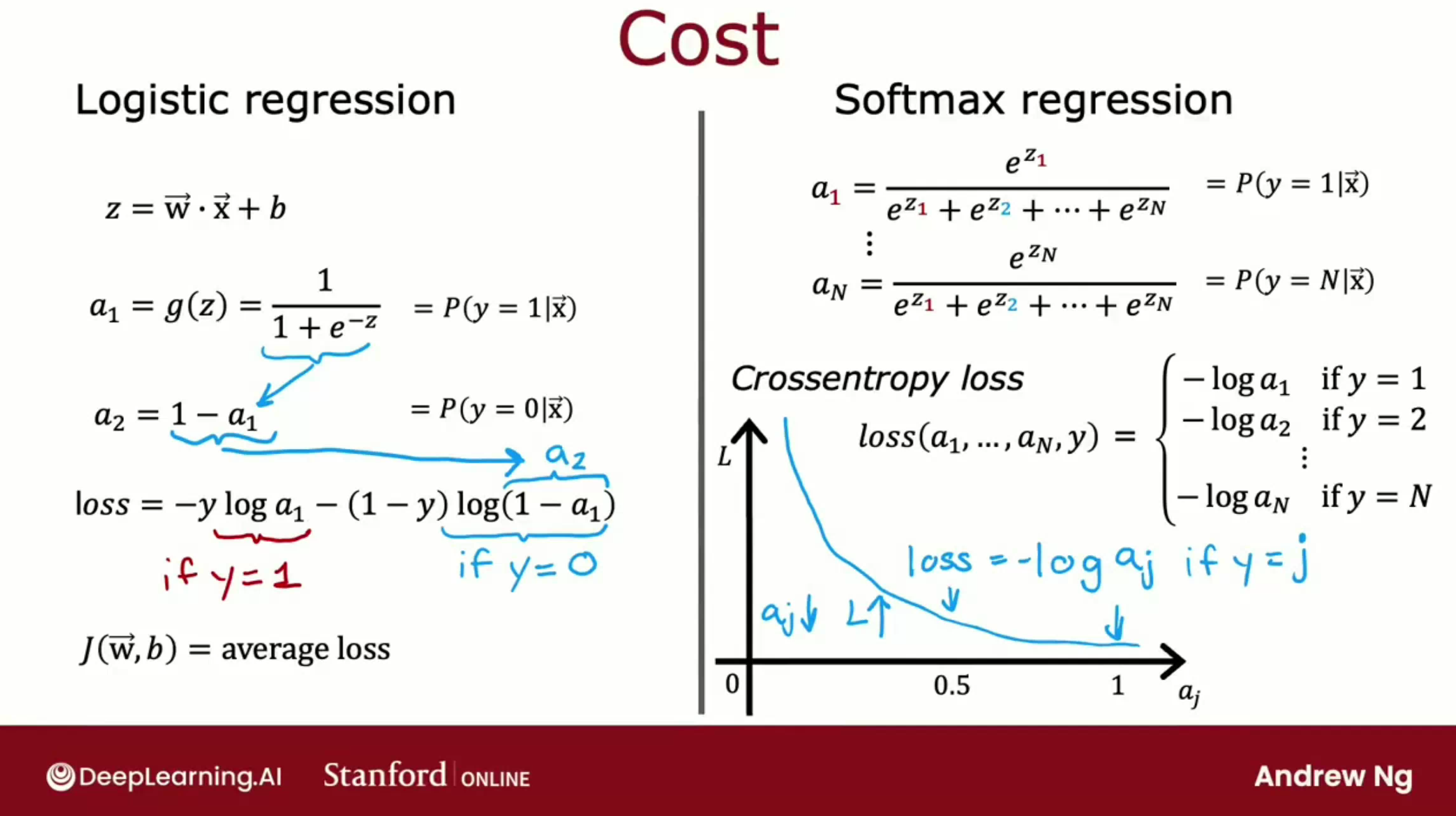
接下来需要将该激活函数放入神经网络中。之前在二分类问题中,输出层为仅含一个激活函数为 Sigmoid 的神经元以输出正类的概率。而在多分类问题中,需要使用新的 Softmax 输出层以输出每一类的概率。因此,与之前的激活函数不同,每一个激活函数为 Softmax 的神经元计算激活值时会用到所有的z1z2..zn。
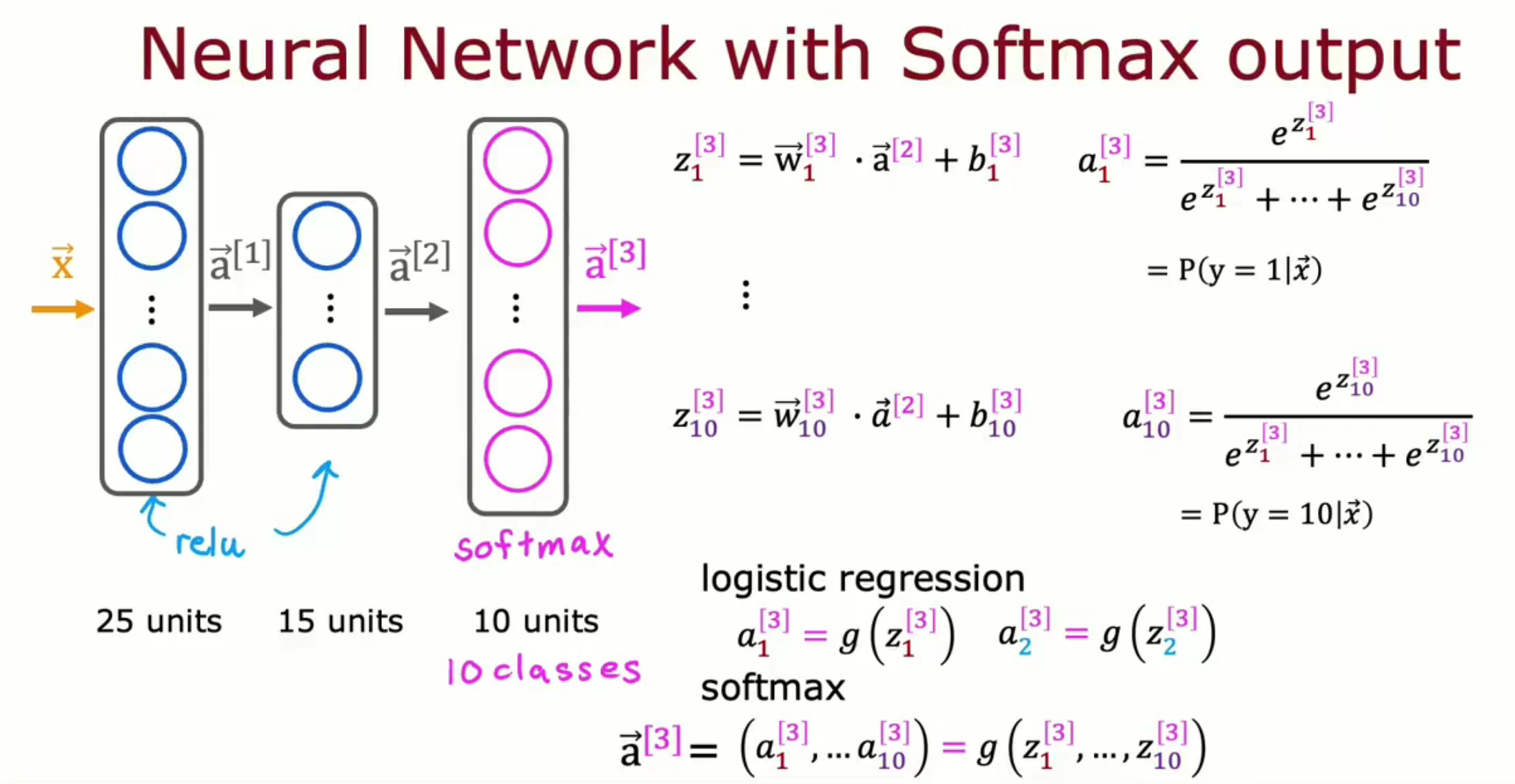
一个十分类问题的代码实现,注意其中十分类问题中 Softmax 层使用了10个神经元,因为该函数接受K个值并输出K个相对概率,3分类问题则需要向该函数输入三个值。因此在十分类问题下该层使用了10个神经元:
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy
model = Sequential([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
Dense(units=10, activation='softmax')
])
# 编译
model.compile(loss=SparseCategoricalCrossentropy())
# 训练模型
model.fit(X, Y, epochs=100)该代码较清晰,但由于会导致四舍五入误差而在工程中不推荐使用。以下是改进处理:
model = Sequential([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
Dense(units=10, activation='linear')
])
model.compile(loss=SparseCategoricalCrossentropy(from_logits=True))
# 训练模型
model.fit(X, Y, epochs=100)
# 预测。由于上一步输出的不再输出a1a2..a10而是输出z1..z10,因此需要将它转为概率
logits = model(X)
f_x = tf.nn.softmax(logits)同理,为避免四舍五入误差,LR也可以使用同样的处理,代码如下:
model = Sequential([
Dense(units=25, activation='sigmoid'),
Dense(units=15, activation='sigmoid'),
Dense(units=1, activation='linear')
])
model.compile(loss=BinaryCrossentropy(from_logits=True))
# 训练模型
model.fit(X, Y, epochs=100)
# 预测
logit = model(X)
f_x = tf.nn.sigmoid(logit)多标签问题
多标签问题指图片中有多个不同类型的目标,这与多分类问题不同。如一张图中同时存在公交车、小汽车、行人等目标。合适的处理方式为训练一个含有多个输出神经元的神经网络。每一个输出神经元仅用于输出一种目标。
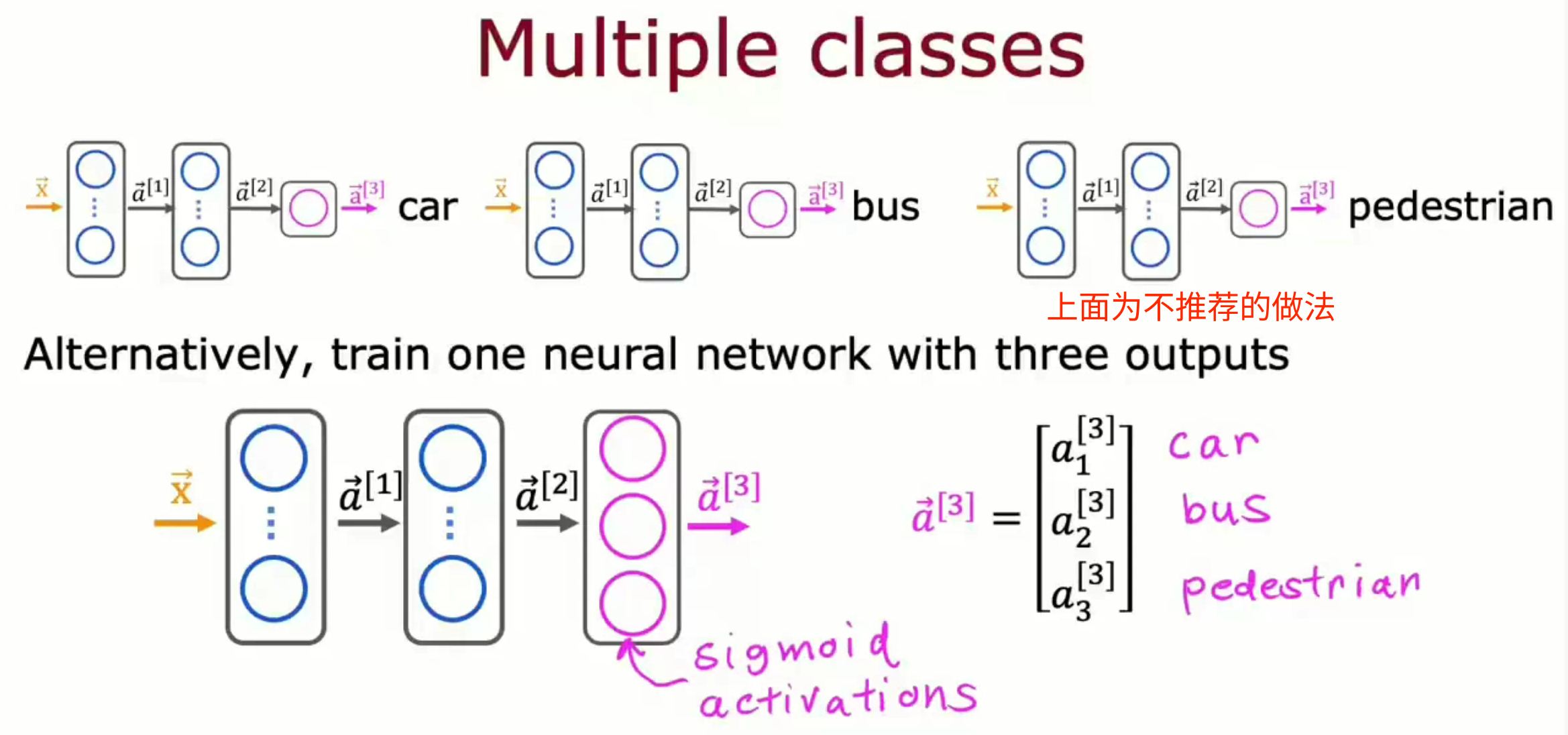
高级优化
自适应矩阵估计算法 Adam 可以自动调整学习率 Learning rate 以进行更快、更平滑的剃度下降。
...
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3), ...)
...# 卷积神经网络
在上文中所有提到的 Dense 层中,每一层都将得到上一层的所有激活值作为输入。然而对于某些应用程序来说,可能Dense层效率不足够高。而卷积层 Convolutional layer 中每个神经元仅将上一层的一部分作为输入。这样使得计算更快,并且更不容易过拟合—训练数据变少了。
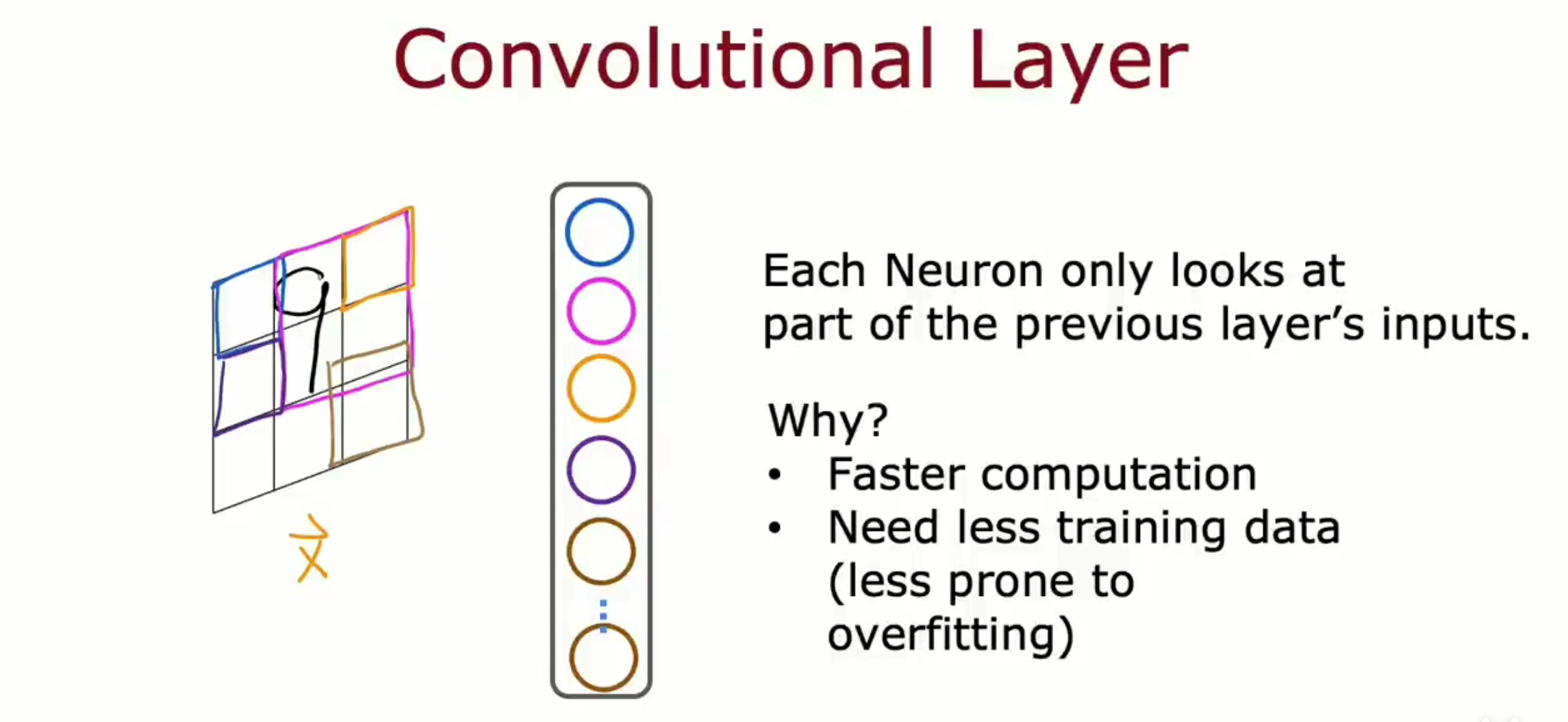
当一个神经网络含有多个卷积层,那么该神经网络被进一步成为卷积神经网络。可以通过设定单个神经元应该查看多大的窗口、每层应有多少个神经元等神经网络架构参数来搭建一个高效的卷积神经网络。
以下图为例,神经网络由一个输入层、两个卷积层、一个输出层构成。其中第一个隐藏层的每个神经元仅关注输入层的一部分,第二个隐藏层中的每个神经元也仅关注第一个隐藏层给的激活向量的一部分。最后一个输出层仅含一个激活函数为 Sigmoid 的神经元以输出患病概率。
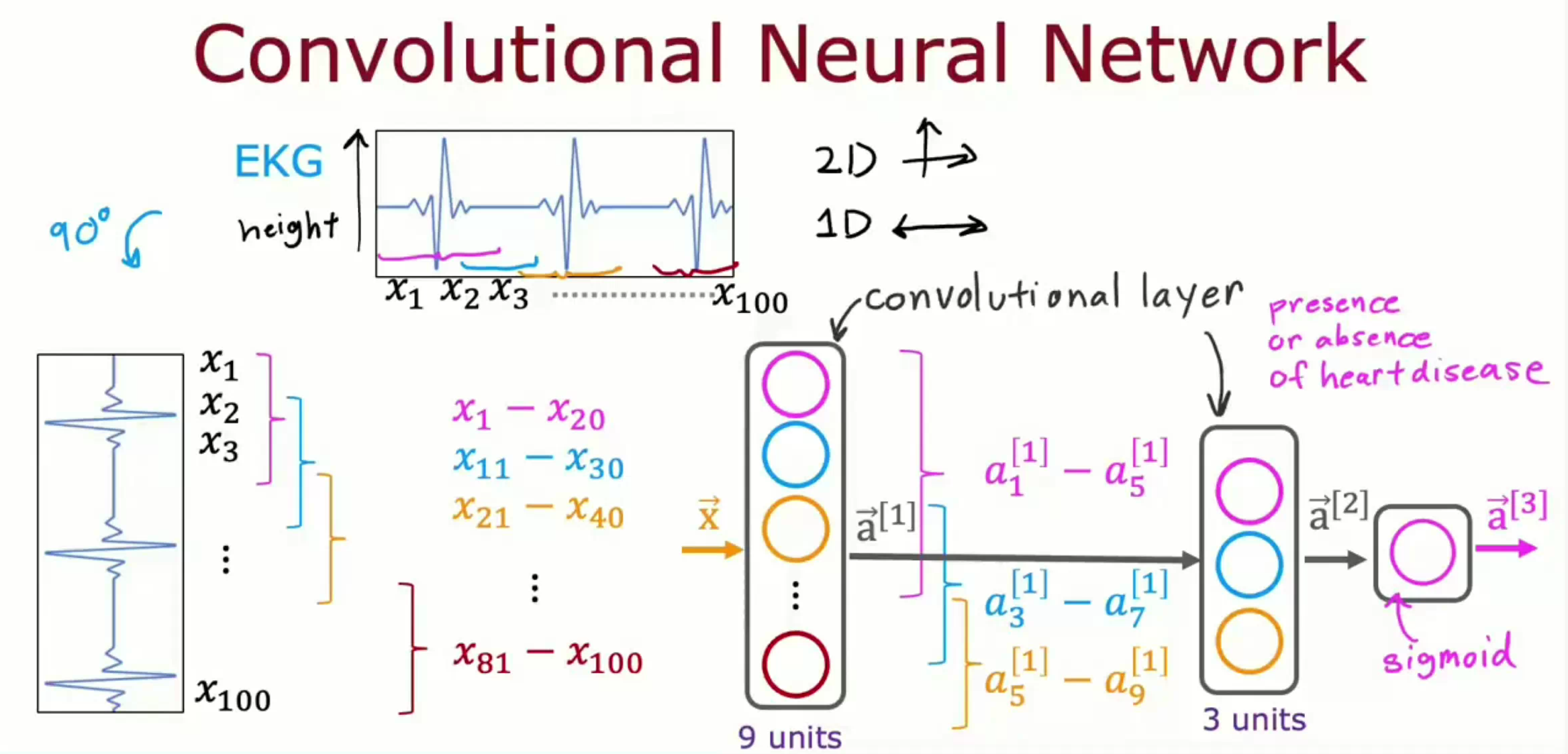
除了卷积层,还有采用自注意力机制的 Transformer ,能够解决长期依赖问题的长短期记忆 Long short-term memory 等等。
# 计算图
计算图将计算的过程用图形表示出来,该图基于数据结构中的图,节点表示变量,边表示变量之间的函数关系。通过计算图可以很形象地描绘很复杂的计算过程。链式法则是复合函数求导的关键规则,也是反向传播的理论基础。过程如下:
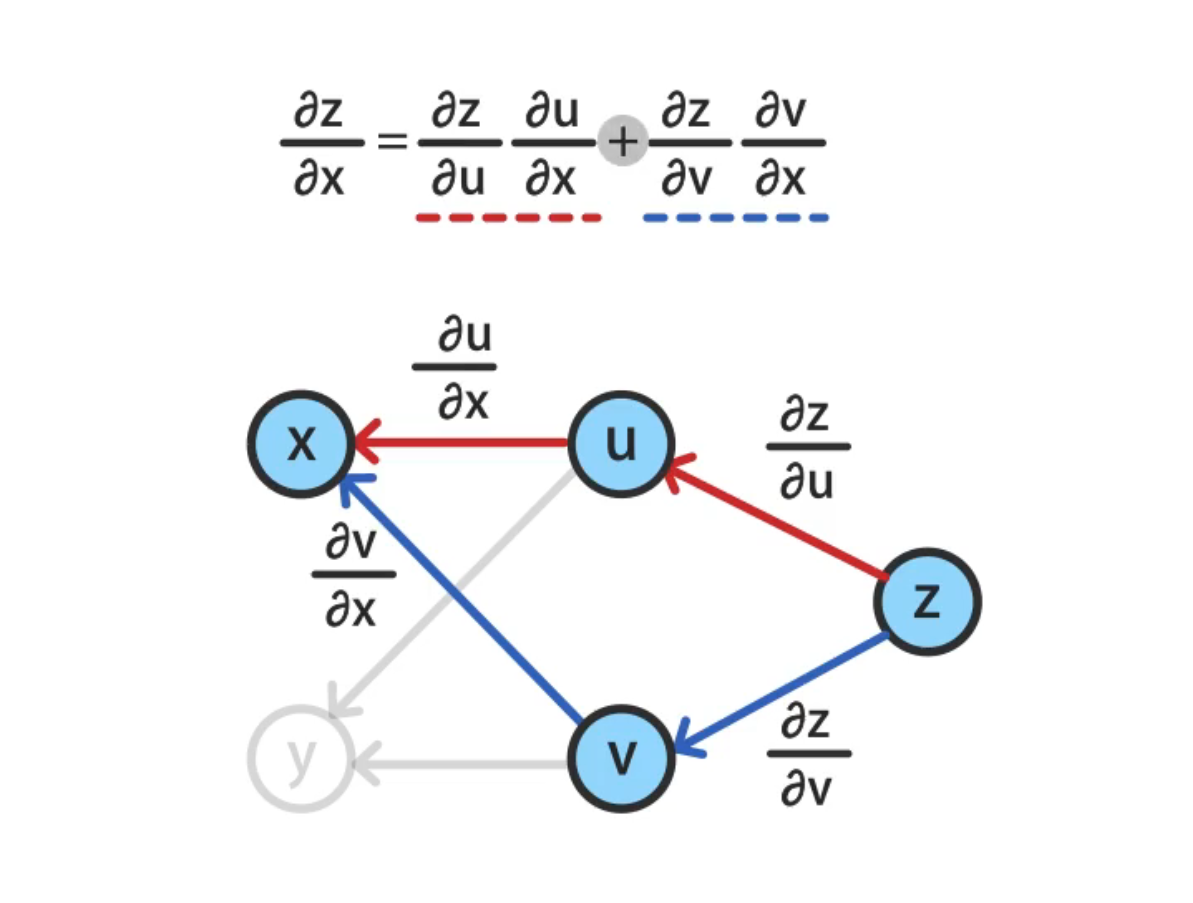
# 神经网络与高方差偏差
阅读该帖理解什么是模型的高偏差、高方差。高方差与高偏差均损害模型的性能。在提到的帖子中也详细介绍了处理高方差与高偏差的方法。结合这些方法,用户还需要在模型高偏差与高方差之间权衡,因为高偏差以为着欠拟合而高方差意味过拟合。
然而对于神经网络这个低偏差机器 low bias machine 来说,在中笔、小笔数据上训练大型神经网络,只要神经网络足够大,则一定能很好拟合数据集。
具体而言:1.先选取一个神经网络架构,试着拟合这笔数据。若 Jtrain 较高则说明存在高偏差,那么试着给神经网络添加隐藏层、给隐藏层添加隐藏神经元。然后再拟合这笔数据,循环该步骤直到很好地拟合这笔数据(达到基准)。2.拟合交叉验证集的数据,观察 Jcv 发现该模型是否存在高偏差问题。若存在,则增加训练集,再回到第一步,循环直到神经网络在交叉验证集上表现良好。
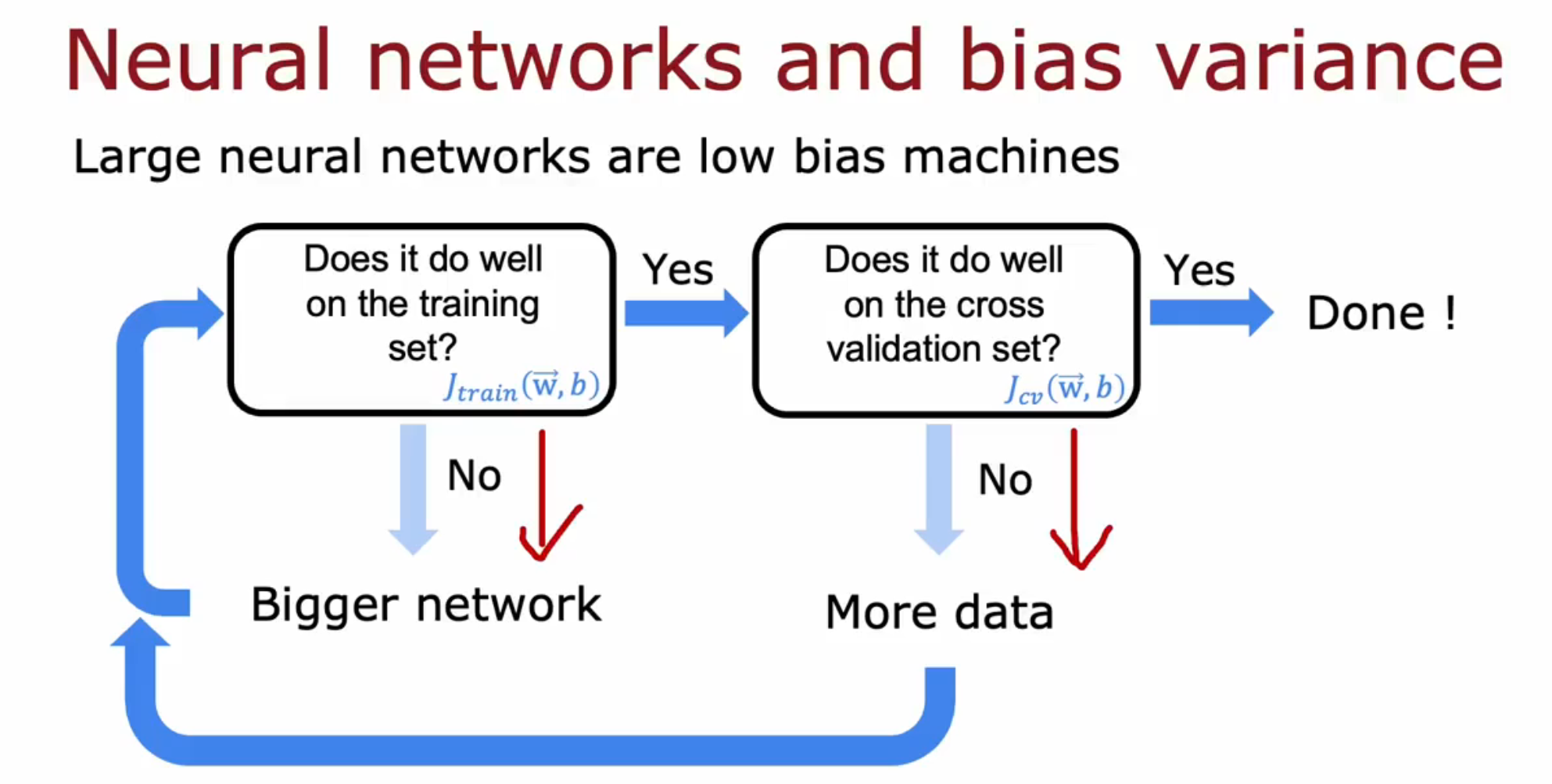
此外,较大的带合适正则化项的神经网络通常比较小的不带正则化项的神经网络表现得更好,或一样好。
神经网络的正则化公式与代码实现:
layer_1 = Dense(units=25, activation='relu', kernel_regularizer=L2(0.01)) # L2(0.01)为正则化系数 layer_2 = Dense(units=15, activation='relu', kernel_regularizer=L2(0.01)) # 每层可以选择不同正则化系数 layer_3 = Dense(units=1, activation='sigmoid', kernel_regularizer=L2(0.01)) model = Sequential([layer_1, layer_2, layer_3])