决策树基础知识比想象的多,因此新开一贴记录决策树最强算法XGBoost。
# 序
本贴不再介绍决策树基础知识、AdaBoost和梯度提升,这些内容在上一则帖子中。该帖主要讲解梯度提升树下的最强库XGBoost。
# 假设函数与弱学习器
XGBoost是采用分布式梯度提升算法框架的开源库,提供的梯度提升算法的假设函数依旧是加法模型:
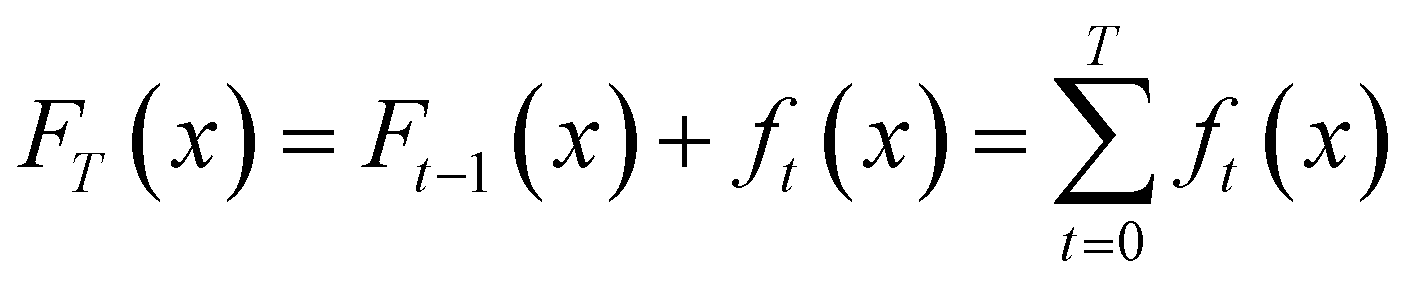
其中,当 t=0 时指的是XGBoost初始化时生成的常量; ft(x) 则为弱学习器——XGBoost回归树,其数学表达式如下:
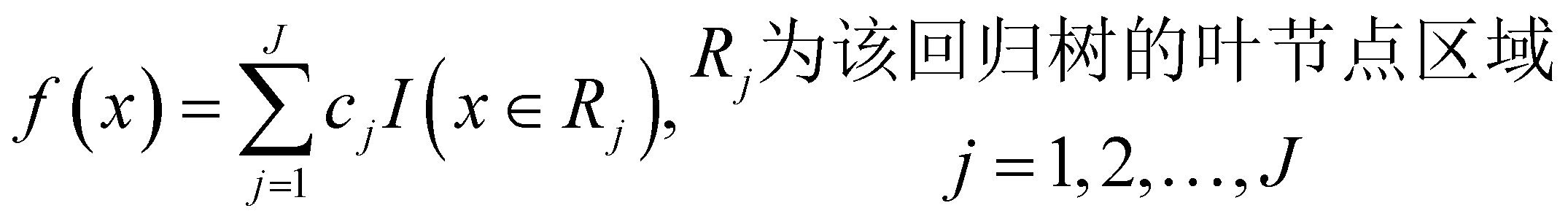
该数学表达式并未展示回归树的形状,仅给出了每个叶节点的输出 cj 。得到树的结构与叶节点输出是XGBoost的任务。
为什么没有学习率?见Shrinkage
# 代价函数与优化目标
上文中给出了XGBoost的假设函数,损失函数依任务类型自行选择:如回归任务选择MSE等损失函数,分类任务选交叉熵损失等函数。弱学习器也在上文中被定义。那么XGBoost的代价函数可以使用下述公式表示:

因此,以该代价函数为目标函数,最小化目标函数得到每棵树的每个叶节点的输出值:

由于XGBoost采用向前分步算法作为优化方法,因此在第t次优化时,之前的弱学习器参数(叶节点输出值)均为常量,而变量只有第t次的参数。目标函数可以进一步表达为:
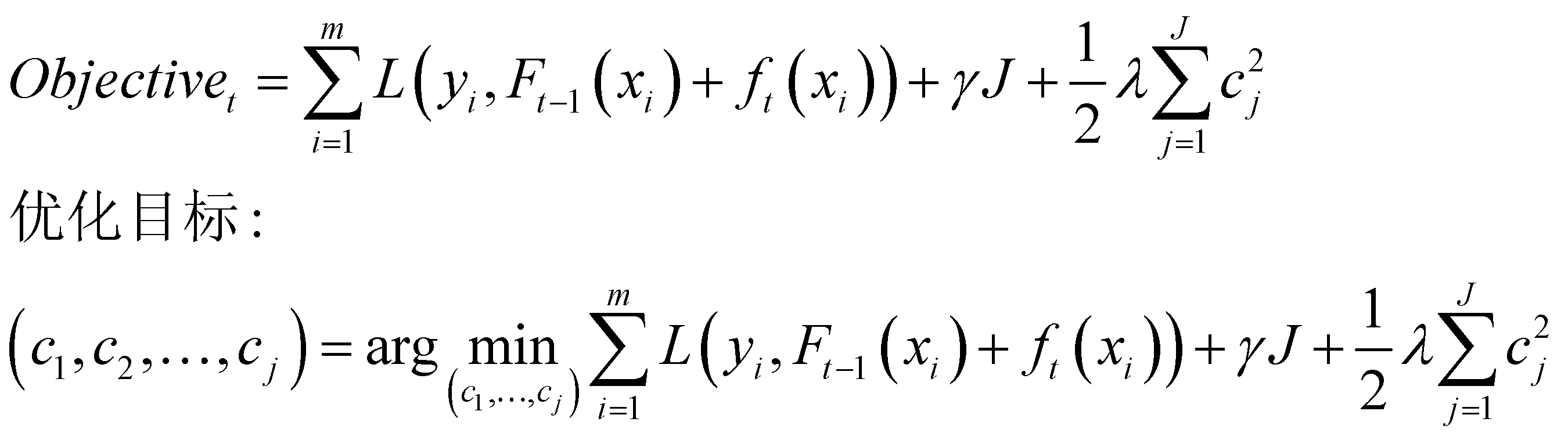
值得注意的是,在拟合第t棵树时,第t棵树并未乘以学习率。学习率是在最后更新加法模型时才出现。
因为损失函数未确定,因此将式子通过二阶泰勒展开并获取第t棵树的优化结果:
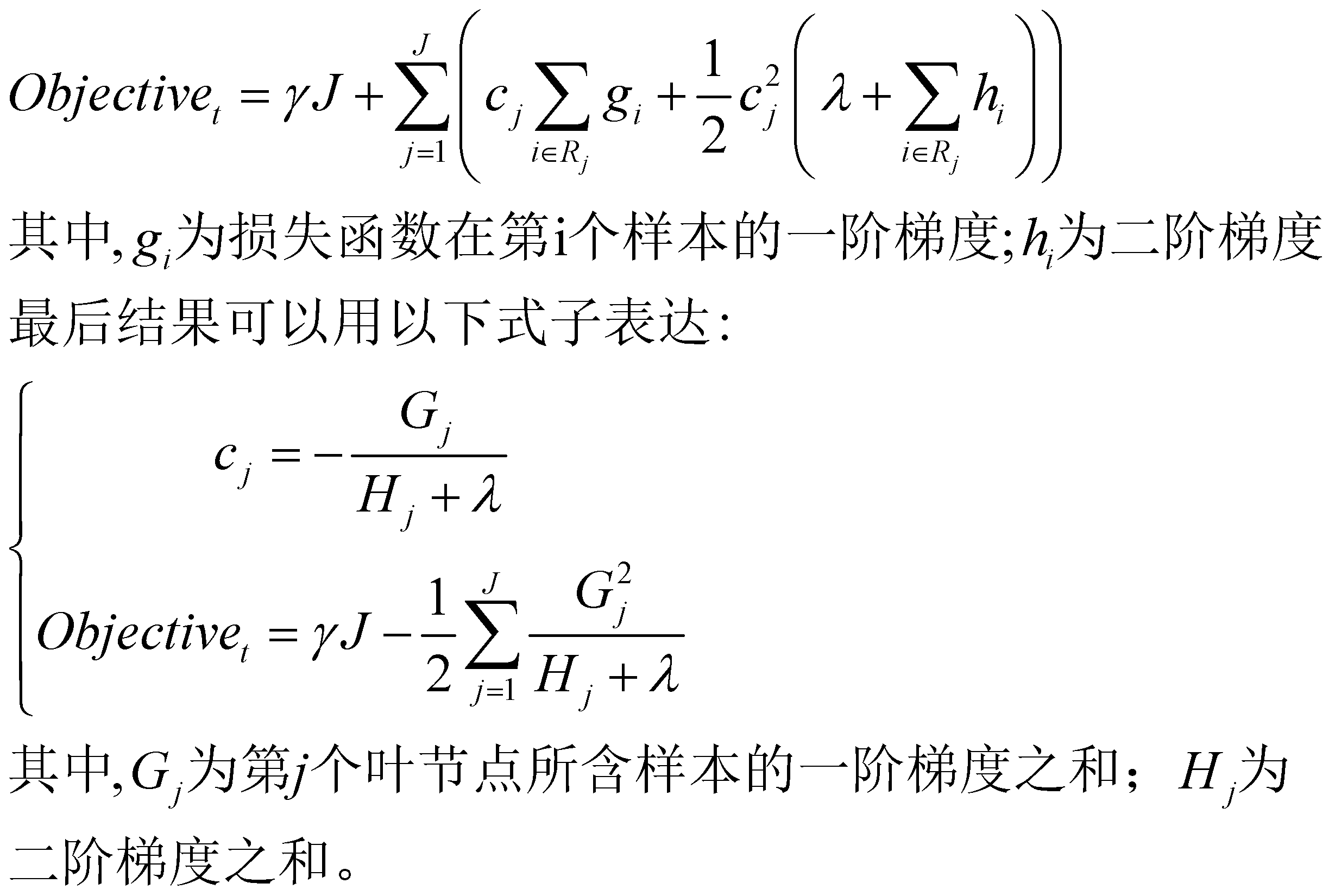
式中, cj 为该次循环中第j个叶节点的输出值。
回归任务和二元分类任务中常见的损失函数
# 树的结构
在XGBoost中,回归树也通过精确贪心算法确定树的分裂,具体而言,通过最大化信息增益的方式确定树的结构。在ID3决策树中,信息增益采用的量化指标为信息熵;而在XGBoost中的回归树中,采用的量化指标为加法模型的代价函数。参考此处以信息熵为例子理解何为最大化信息增益。
与ID3不同的是,梯度提升树中不再考虑左右分支样本数量占比,而是简单了当计算上图中的 Objective 来量化信息增益:
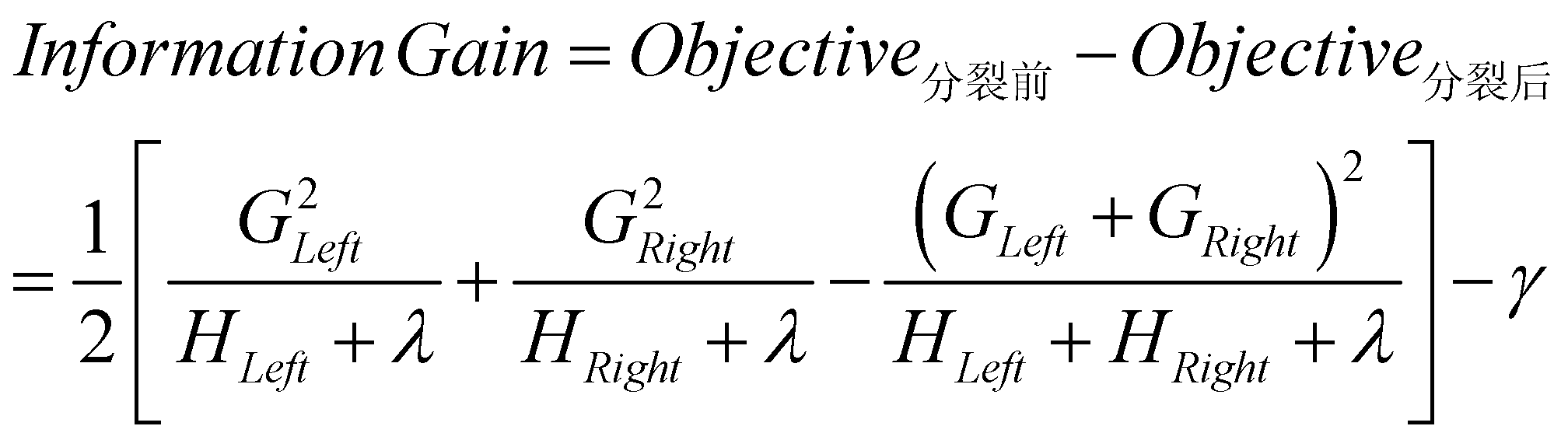
式中, GLeft 是以该特征为分裂点时损失函数在左侧分支所含样本的一阶梯度之和; GRight 是以该特征为分裂点时损失函数在右侧分支所含样本的一阶梯度之和; HLeft 是以该特征为分裂点时损失函数在左侧分支所含样本的二阶梯度之和; HRight 是以该特征为分裂点时损失函数在右侧分支所含样本的二阶梯度之和。
选取使得信息增益最大的特征作为分裂点。
贪心算法,换句话说是一种保证每一步都为最优解从而达到全局最优解的方法。在决策树的构建中表现为:保证每一次节点的分裂产生的新的树,都使得目标函数值最小。
# 优化
XGBoost又快又准的原因之一是在构建决策树的过程中引入了对特征和对特征值的采样。
对特征进行采样
太多的特征使得建树时间较长,因此XGBoost使用列采样的方法对特征进行采样,以减少建树时长。列采样又分按树采样和按层采样:
按树采样
先在特征空间中进行随机采样,选取得到的特征进行整棵树的构建。
按层采样
在每层节点的构建之前均对特征进行一次随机采样,选取得到的特征进行该层节点的构建。其中,一个分支内同一深度的节点为同一层的节点。
对特征值进行采样
抽样选取或者全选特征后,可以采用加权分位法 Weighted Quantile Sketch 选取特征值,按抽样获得的特征值进行建树,进一步减少算法耗时。加权指的是以损失函数在该样本的二阶梯度作为该样本的权重,换句话说,以该二阶梯度作为该样本出现的次数。采用加权分位法的原因是样本分布并不均匀,公式来自代价函数二阶泰勒展开的变形。
如, h3=2 指损失函数在第3个样本的二阶梯度为二,则第三个样本的权重为二——将第3个样本复制为二个。以此类推计算损失函数在所有样本的二阶梯度并以此对样本进行赋权,然后进行归一化——让所有样本的权重加起来为1。
给定一个 ε 使得抽样得到的特征值切得的范围不得超过该值,对应的公式在图中。
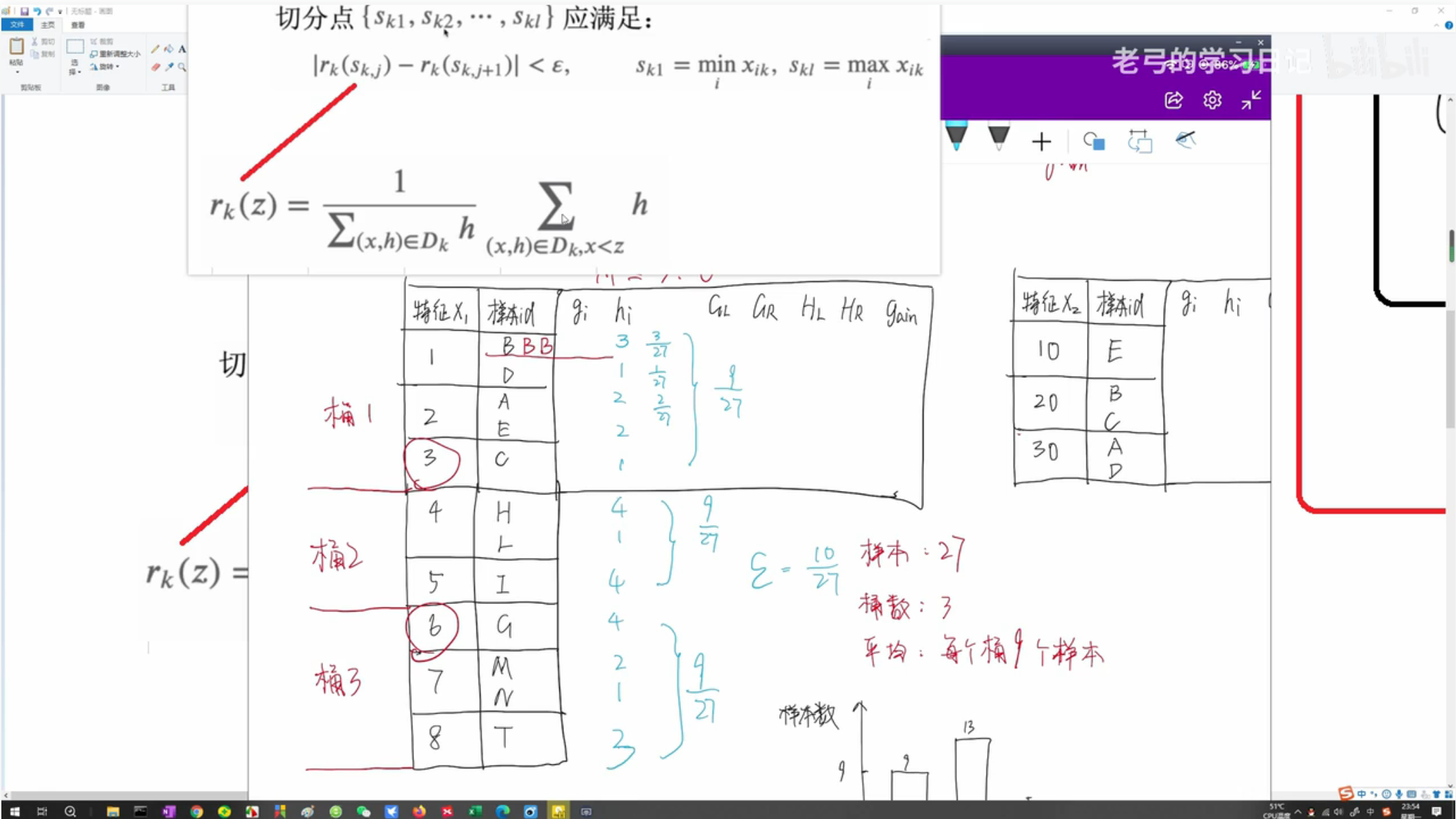
建树时特征值采样策略
在建树时特征值采样有两种策略:①全局策略;②局部策略。与上文中的按树采样和按层采样意思相近,前者指一旦特征值采样完成,整棵树每个节点的构建均使用这些特征值;后者指每个节点进行分裂时均按加权分位法重新采样得到特征值。同ε下,局部策略的效果优于全局策略。
# 缺失值处理
XGBoost可以处理缺失值,其方法是:先将所有具有缺失值的样本(将缺失值样本看作一个整体)放到左侧分支,得到一个增益。再放到右侧分支,并且同样的到一个增益。对比两者谁更大,将所有缺失值样本放到使增益较大的一侧。
值得注意的是,缺失值样本不参与利用加权分位数算法进行的特征值选择。
该缺失值处理的方法被称为稀疏自适应划分点查找 Sparsity-Aware Split Finding 。
# Shrinkage
在文章开头给出的数学公式中并未提到学习率(步长),因为给出的是加性模型的通用数学公式。XGBoost引入了学习率,通常被称为收缩 Shrinkage ,旨在防止过拟合。更新加法模型之前,先将拟合得到的弱学习器乘以学习率:
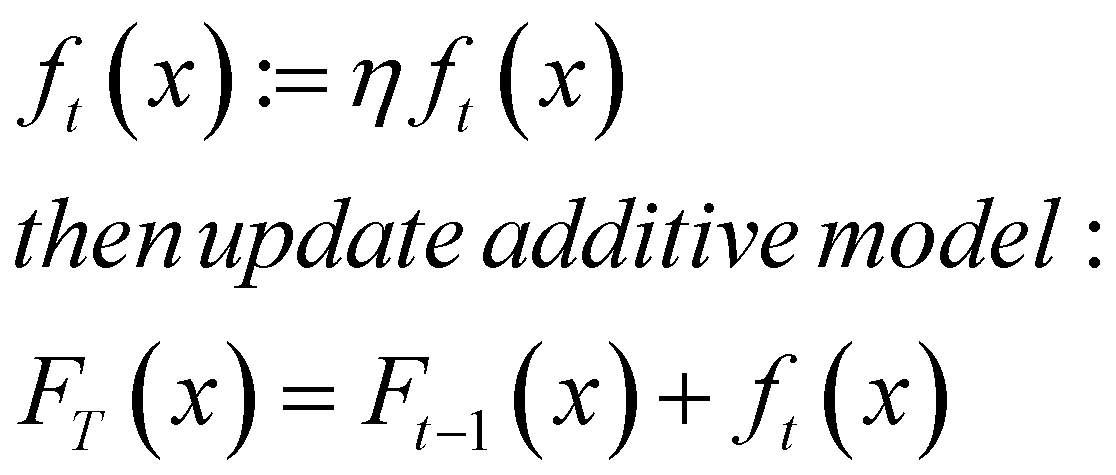
# 算法流程
使用XGBoost处理回归及分类任务的算法流程几乎一致。
回归任务
初始化 f0(x)=0.5 或等于训练集中所有样本目标变量的均值。
# 代码实现
以下代码实现通过 XGBoost 进行分类:
from xgboost import XGBClassifier model = XGBClassifier() model.fit(X_train, y_train) y_pred = model.predict(X_test)
以下代码实现通过 XGBoost 进行回归:
from xgboost import XGBRegressor model = XGBRegressor() model.fit(X_train, y_train) y_pred = model.predict(X_test)
