做些练习加强理解。
# 线性回归分析
在统计学中,回归分析指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
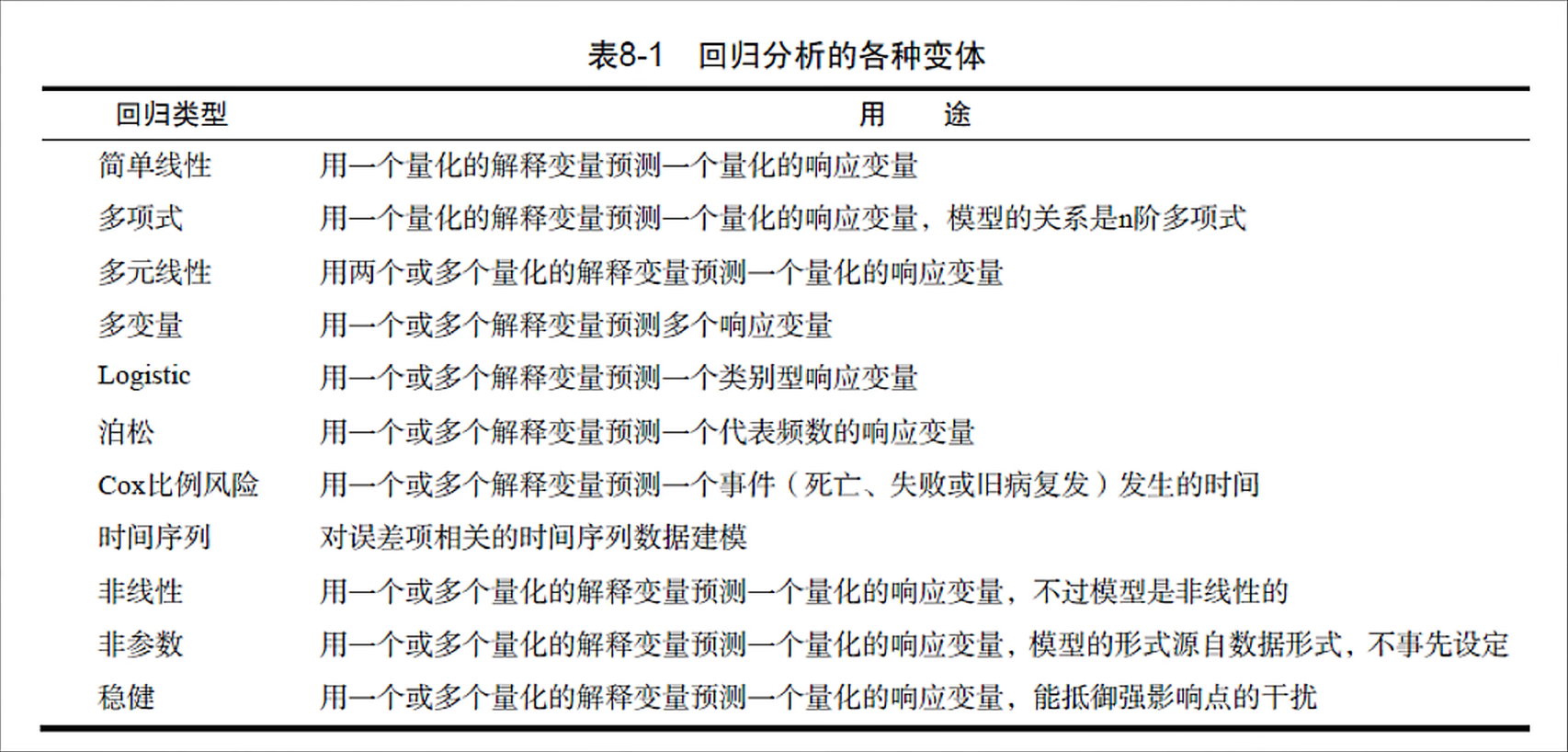
这里先介绍最简单的线性回归。利用普通最小二乘法(OLS)。
fit <- lm(women$weight ~ women$height)
summary(fit)
输出:这里Call则是formula,Residual是残差,Intercept是截距(x=0时,y的值),它下面那个是系数。Residual Standard Error是标准误。
Multiple R-squared是R方判定系数,是衡量模型拟合质量的指标,取值0-1之间,值越大拟合越好。意思是可以解释99.1%的数据,只有0.9%的数据不符合这个模型。
F-statistic是F统计量,说明模型是否显著,用p-value衡量,p-value越小,模型越显著。
Call:
lm(formula = women$weight ~ women$height)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
women$height 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14所以在观察结果的时候,先看F-statistic的p-value,如果不小于0.05,这个模型就没价值了,需要重新拟合。
如果F统计的p-value小于0.05,则去看R方,看看模型能解释多少变量。
可以用以下函数来查看lm()函数的结果。

confint(fit, level = 0.5) //置信区间改成50%
输出:
25 % 75 %
(Intercept) -91.635892 -83.397441
women$height 3.386767 3.513233如果想把回归取线绘制在散点图上,可以用低级绘图函数来描绘。
fit <- lm(women$weight ~ women$height)
plot(women$height, women$weight) //绘制散点图
abline(fit) //低级绘图函数,把回归线绘上去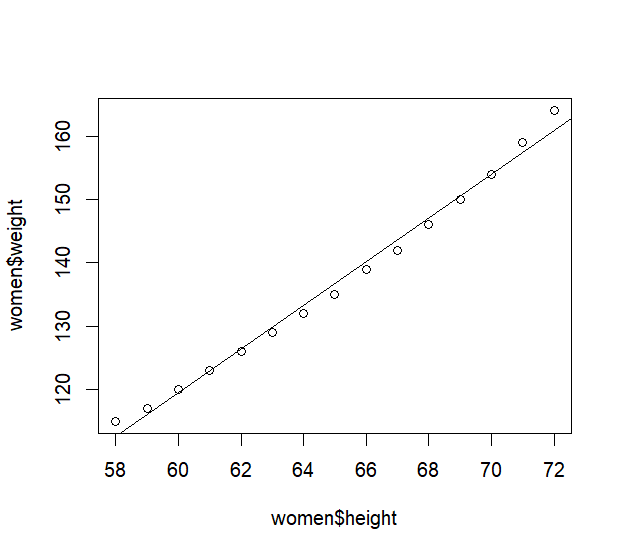
就身高体重这个问题,利用多项式回归试试
fit2 <- lm(weight ~ height + I(height^2), data = women) //之后会得到系数,回归方程就把系数乘以项再加起来,就是回归方程了
plot(women$height, women$weight)
abline(fit) //绘制直线的低级绘图函数是abline()
lines(women$height, fitted(fit2), col = "red") //绘制曲线的低级绘图函数是lines(), lines()是根据x和y来绘线。这里height就是x,拟合值就是y。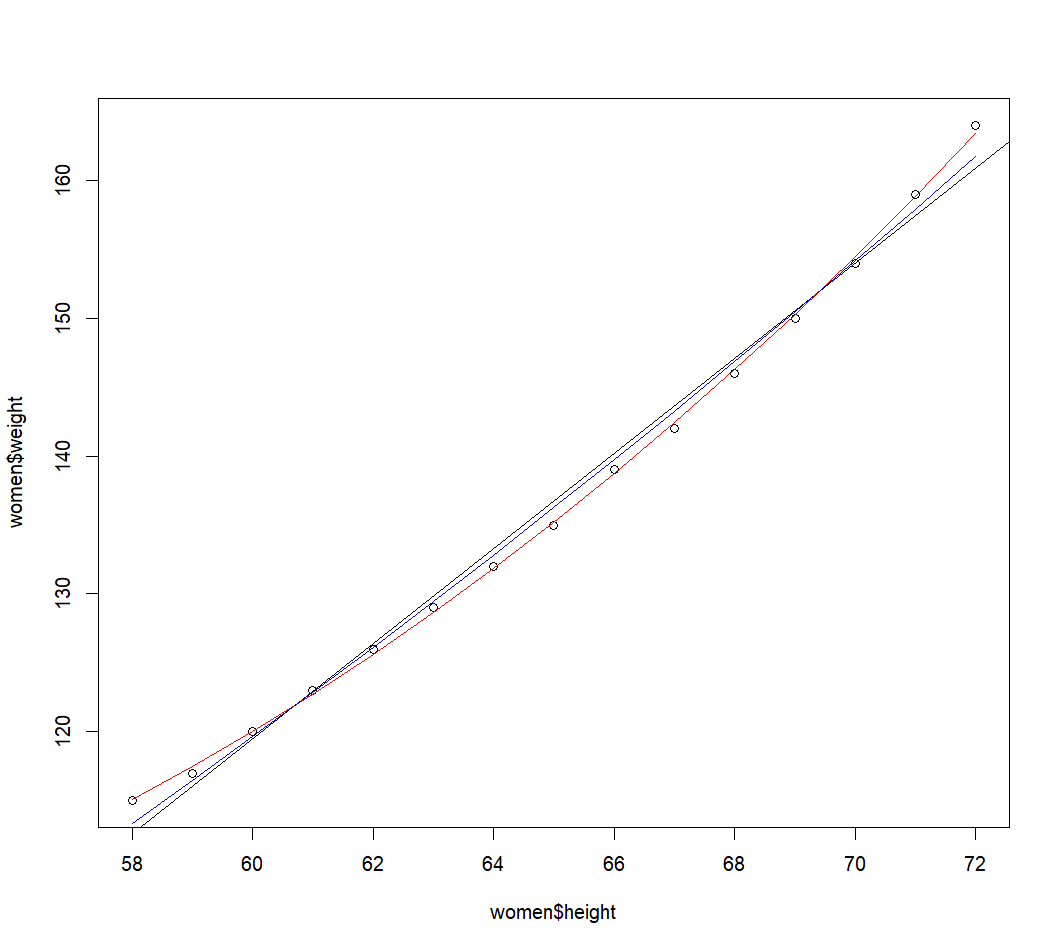
# 多元线性回归
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
statesDf <- as.data.frame(state.x77[,c(5,1,3,2,7)]) //只用这几列数据进行多元回归分析
fit <- lm(Murder ~ Population+Illiteracy+Income+Frost, data = statesDf) //进行多元回归分析
summary(fit)
输出:在Coefficient那一块,有对应的系数,星星越多越显著。比如文盲率那一块就是4.143*Illiteracy。根据Intercept(截距)和那些系数,就能写出方程了
Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost,
data = statesDf)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08再举一个复杂的例子。
fit <- lm(mpg ~ hp+wt+hp:wt, data = mtcars) //hp:wt指hp和wt的交互项,但具体不知道是如何交互的
summary(fit)
输出:可以看到,hp和wt的交互项的显著性也很强
Call:
lm(formula = mpg ~ hp + wt + hp:wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.0632 -1.6491 -0.7362 1.4211 4.5513
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.80842 3.60516 13.816 5.01e-14 ***
hp -0.12010 0.02470 -4.863 4.04e-05 ***
wt -8.21662 1.26971 -6.471 5.20e-07 ***
hp:wt 0.02785 0.00742 3.753 0.000811 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.153 on 28 degrees of freedom
Multiple R-squared: 0.8848, Adjusted R-squared: 0.8724
F-statistic: 71.66 on 3 and 28 DF, p-value: 2.981e-13但是,如果变量很多的话,具体该怎么办呢?
states <- as.data.frame(state.x77[,c("Murder", "Population", "Income", "Frost", "Illiteracy")])
fit1 <- lm(Murder ~ Population+Illiteracy+Income+Frost,data = states)
fit2 <- lm(Murder ~ Population+Illiteracy, data = states)
AIC(fit1,fit2)
输出:fit2的AIC值更小,拟合更好。越小就说明模型用较少的参数获得足够的拟合度。
df AIC
fit1 6 241.6429
fit2 4 237.6565如果变量更多的话,显然AIC也不行了。对于变量的选择就需要用逐步回归法、全子集回归法。
在逐步回归法中,模型会一次增加或者删除一个变量,直到达到继续增加或删除变量时模型不再发生变化这个节点。如果每次是增加变量,则是向前逐步回归。如果是每次删除变量,则是向后逐步回归。
全子集回归法是取所有可能的模型,从中计算出最佳的模型。
leaps <- regsubsets(Murder ~ Population+Illiteracy+Income+Frost, data = states, nbest = 4)
输出:
Call: regsubsets.formula(Murder ~ Population + Illiteracy + Income +
Frost, data = states, nbest = 4)
4 Variables (and intercept)
Forced in Forced out
Population FALSE FALSE
Illiteracy FALSE FALSE
Income FALSE FALSE
Frost FALSE FALSE
4 subsets of each size up to 4
Selection Algorithm: exhaustive
Population Illiteracy Income Frost
1 ( 1 ) " " "*" " " " "
1 ( 2 ) " " " " " " "*"
1 ( 3 ) "*" " " " " " "
1 ( 4 ) " " " " "*" " "
2 ( 1 ) "*" "*" " " " "
2 ( 2 ) " " "*" " " "*"
2 ( 3 ) " " "*" "*" " "
2 ( 4 ) "*" " " " " "*"
3 ( 1 ) "*" "*" "*" " "
3 ( 2 ) "*" "*" " " "*"
3 ( 3 ) " " "*" "*" "*"
3 ( 4 ) "*" " " "*" "*"
4 ( 1 ) "*" "*" "*" "*" # 回归诊断
做回归只是开始,比如模型是否是最佳模型、模型多大程度满足OSL模型的统计假设、模型是否经得起更多数据的检验、如果拟合的指标不好怎么办等待,都是要解决的问题。
除了使用 summary() 函数查看拟合指标,还可以使用 plot() 函数绘图来查看拟合结果。
以women数据集为例
fit <- lm(weight ~ height, data = women)
par(mfrow = c(2,2)) //par()函数对全局起作用
plot(fit)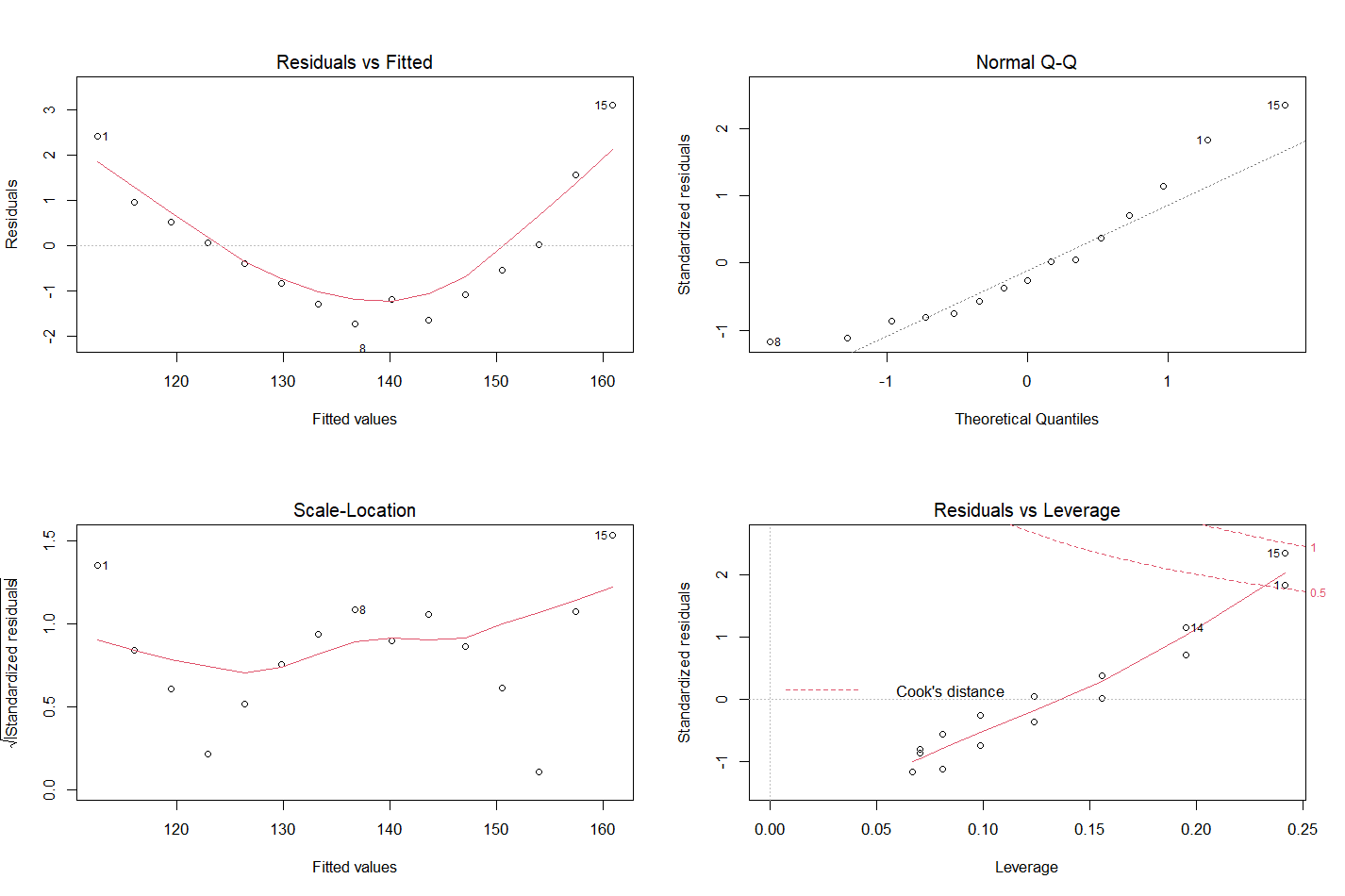
第一幅图是残差与拟合的图,评价因变量和自变量是否成线性关系,曲线为拟合曲线。如果是取线的话,说明可能存在二次项的分布。
第二幅图描述正态性,如果数据成正态分布,在QQ图则是一条直线。
第三幅图是位置与尺寸图,描述同方差性,如果满足同方差性,则点应该在水平线周围随机分布。
第四幅图是残差与杠杆图,提供对单个数据值的观测,鉴别离群点(不适合模型的点),杠杆点(异常的预测变量的组合),强影响点(这个值对模型参数的估计产生的影响过大,可以用Cook’s distance来鉴别)。如果将这些点删除掉,拟合的结果会更好。但…
抽样法验证:
这也是比较好的方法。
- 如数据集有1000个样本,随机抽取500个进行回归分析
- 模型建好后,利用predict()函数对剩下500个样本进行预测,与剩下500个样本比较残差值
- 如果预测准确,说明模型可以,否则需要调整模型
# 方差分析
方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”,用于两个及两个以上样本均数差别的显著性检验。 由于各种因素的影响,研究所得的数据呈现波动状。造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
单因素方差分析:
使用 multcomp 包的数据集来做这个分析。cholesterol数据集是50个患者接受治疗,分为5组,一组10人。每一组分别进行A药物1天1次服用,A药物1天分两次服用,A药物一天分4次服用,B药物和C药物。然后确定药物的效果。
数据集只有两列,一列记录怎么治疗,一列显示药物持续时间。一般来说只需要算每一组的平均值,比一比哪个最长就行了。但我们需要知道这个差别,是来自组间还是组内。如果是组间的差距的话,那么就证明确实那一组响应时间最长的治疗效果更好。
?cholesterol //这个数据是50个患者分成10人一组,接受药物治疗。数据只有一列治疗方式和一列响应时间
aggregate(cholesterol$response, by = list(cholesterol$trt), FUN = mean)
aov1 <- aov(response ~ trt, data = cholesterol)
summary(aov1)
输出:F值越大,组间差异越显著。P值越小,F值越可靠
Df Sum Sq Mean Sq F value Pr(>F)
trt 4 1351.4 337.8 32.43 9.82e-13 ***
Residuals 45 468.8 10.4
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1双因素方差分析:
使用ToothGrowth数据集,60只豚鼠分别采取两种维C和橙汁喂食方法,每种喂食方法种,抗坏栓含量有3个水平。
每组选10只豚鼠。牙齿生长为因变量。
aggregate(ToothGrowth$len, by = list("喂食" = ToothGrowth$supp, "剂量" = ToothGrowth$dose), FUN = mean)
dose1 <- as.factor(ToothGrowth$dose) //aov函数需要用因子来计算
aov1 <- aov(len ~ supp*dose1, data = ToothGrowth) //因为橙汁里含有VC,所以这两项有交互,用*
summary(aov1)
输出:喂食和剂量的结果都很显著(三颗星),说明不同喂食方法和剂量对牙齿生长都有影响
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 15.572 0.000231 ***
dose1 2 2426.4 1213.2 92.000 < 2e-16 ***
supp:dose1 2 108.3 54.2 4.107 0.021860 *
Residuals 54 712.1 13.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
对于这个结果可以用HH::interaction.plot()函数绘制出来
interaction.plot(dose1, ToothGrowth$supp, ToothGrowth$len, type = "b", col = c("red", "blue"), pch = c(16,18), main = "Interaction between Dose and Supplement Type")
输出: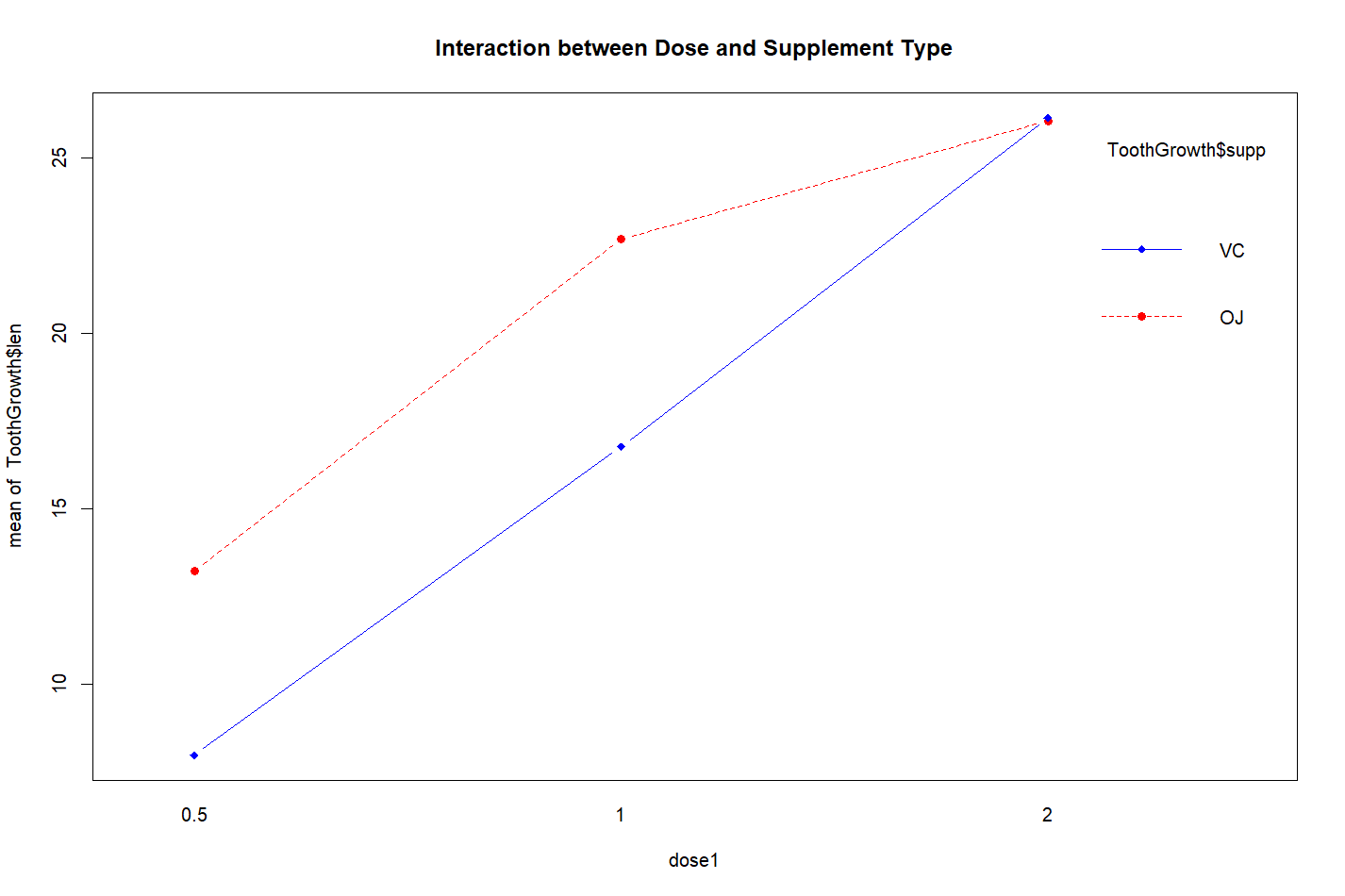
这幅图得出,刚开始橙汁的效果明显,当剂量达到2mg时,二者的效果就相同了。
协方差分析:
单因素协方差分析的例子:
使用mulcomp包litter的数据。是怀孕小鼠的数据,74个小鼠分为4组。分别进行0、5、50、500单位计量进行试验。因为怀孕的总时间有差别,这会影响幼崽体重,所以属于协变量。
aggregate(litter$weight, by = list(litter$dose), FUN = mean) //可见,按照计量来分组,输出的是体重的均值。每一组(不同剂量)均值不同。
那么每一组的组间是否为显著差别?因此需要用协方差分析来计算
aggregate(litter$weight, by = list(litter$dose), FUN = mean)
aov1 <- aov(weight ~ gesttime+dose, data = litter) //协变量(gesttime)放在自变量前面
summary(aov1)
输出:dose的F值有一颗星。怀孕时间与出生体重相关,控制怀孕时间,出生体重与剂量相关,说明药物是有影响的不是随机产生的
Df Sum Sq Mean Sq F value Pr(>F)
gesttime 1 134.3 134.30 8.049 0.00597 **
dose 3 137.1 45.71 2.739 0.04988 *
Residuals 69 1151.3 16.69
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1多元方差分析:
shelf1 <- as.factor(UScereal$shelf) //aggregate()函数,应该用因子来分类,所以转换成因子
aggregate(cbind("calories" = UScereal$calories, "fat" = UScereal$fat, "sugars" = UScereal$sugars), by = list(shelf1), FUN = mean) //aggregate()函数是将xx用xx因子分类,所以用cbind()把前面的xx都合并成一个对象
manova1 <- manova.(cbind("calories" = UScereal$calories, "fat" = UScereal$fat, "sugars" = UScereal$sugars) ~ shelf1)
summary.aov(manova1)
输出:可以发现每组结果差异是显著的。
Response calories :
Df Sum Sq Mean Sq F value Pr(>F)
shelf1 2 50435 25217.6 7.8623 0.0009054 ***
Residuals 62 198860 3207.4
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Response fat :
Df Sum Sq Mean Sq F value Pr(>F)
shelf1 2 18.44 9.2199 3.6828 0.03081 *
Residuals 62 155.22 2.5035
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Response sugars :
Df Sum Sq Mean Sq F value Pr(>F)
shelf1 2 381.33 190.667 6.5752 0.002572 **
Residuals 62 1797.87 28.998
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1# 功效分析
可以帮助在给定置信度的情况下,判断检测到给定效应值所需的样本量,反过来,也可以在给定置信度水平情况下,计算在某样本量内能检测到给定效率值的概率。如果概率低的难以接受,则需要对实验进行调整。
功效分析是个交互性的过程,研究者通过改变样本量、预期显著性水平、预期功效水平等参数,来观察它们对其他参数的影响。过去研究的信息可以帮助在未来设计给高效的实验。
功效分析的理论基础:

这里没听懂,以后再看看。
运用:
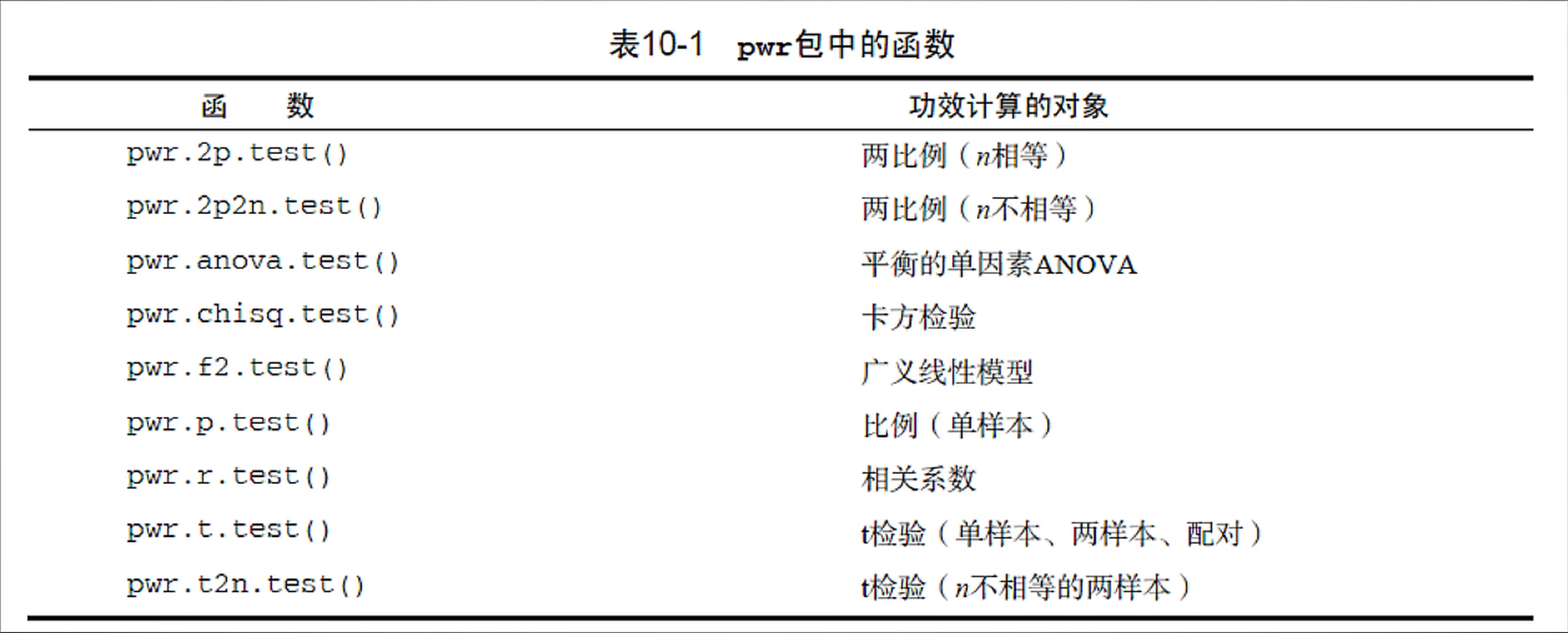
进行功效分析,可以使用pwr包,根据不同的假设检验选择不同的函数。
举一个线性回归功效分析的案例:
线性回归功效分析可以使用pwr::pwr.f2.test()函数,其中sig.level表示显著性水平,默认为0.05,power为功效水平
pwr.f2.test(u = 3, sig.level = 0.05, power = 0.9, f2 = 0.0769) //假定显著性水平为0.05。f2是需要计算得出的
输出:假定显著性水平为0.05,v = 184.2426,则说明需要185个样本
Multiple regression power calculation
u = 3
v = 184.2426
f2 = 0.0769
sig.level = 0.05
power = 0.9# 广义线性模型
前面的线性回归和方差分析都是基于正态分布的假设。在线性模型中,可以通过一系列连续型或类别型变量来预测响应变量。但在实际数据分析中,绝大部分数据都是无规则分布的。
通过 glm() 函数可以对非正态因变量的分析。
泊松回归:
泊松回归是用来为计数资料和列联表建模的一种回归分析。泊松回归假设因变量是符合泊松分布的,并假设它平均值的对数可以被未知参数的线性组合建模。常用于对体育赛事的预测。
data(breslow.dat, package = "robust")
attach(breslow.dat)
fit <- glm(sumY ~ Base+Trt+Age, data = breslow.dat, family = poisson(link = "log")) //这是广义回归模型中,泊松回归的写法,可以用help()查看帮助,里面有写。
summary(fit)
输出:在泊松回归中,因变量以条件均值的对数形式建模,年龄的回归系数为0.0227,这表示保持其他预测变量不变,年龄每增加一岁,则癫痫病发病数的对数均值将增加0.0227.当预测变量都为0时没有意义,因为年龄不可能为0,因此截距没有意义。
这里输出的都是均值的对数,可以用exp(coef(fit))取指数。
Call:
glm(formula = sumY ~ Base + Trt + Age, family = poisson(link = "log"),
data = breslow.dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-6.0569 -2.0433 -0.9397 0.7929 11.0061
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.9488259 0.1356191 14.370 < 2e-16 ***
Base 0.0226517 0.0005093 44.476 < 2e-16 ***
Trtprogabide -0.1527009 0.0478051 -3.194 0.0014 **
Age 0.0227401 0.0040240 5.651 1.59e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2122.73 on 58 degrees of freedom
Residual deviance: 559.44 on 55 degrees of freedom
AIC: 850.71
Number of Fisher Scoring iterations: 5
# Logistic回归
Logistic回归分析是广义线性回归分析的一种。单独讲,因为之后要用到。当用一系列连续型或类别型预测变量来预测二值型结果变量时,Logistic回归是一个非常有用的工具。
例如:想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里因变量就是是否有胃癌,即二值型变量。自变量就包括很多了,例如性别、年龄、饮食习惯、幽门螺旋杆菌感染等。自变量既可以是连续的也可以是分类的。通过Logistic回归分析,就可以了解到哪些因素是胃癌的危险因素。
因为结果需要时二值型变量,所需需要转换一下数据结果,把结果改为0或1。
Affairs$YnAffairs[Affairs$affairs > 0] <- 1 //重新定义一列,只要出轨了无论几次都记作1
Affairs$YnAffairs[Affairs$affairs == 0] <- 0 //没有出轨就记作0
Affairs$YnAffairs <- factor(Affairs$YnAffairs, levels = c(0,1), labels = c("No", "Yes")) //注意这个factor()不是as.factor(),不是转换成factor,而是直接生成新的factor数据类型把原数据覆盖了。这样YnAffairs的值就是Yes和No了,而不是0和1
attach(Affairs) //把数据集Attach进来方便输入,用完后记得Detach
lofit <- glm(YnAffairs ~ gender+age+yearsmarried+children+religiousness+education+occupation+rating, data = Affairs, family = binomial(link = "logit")) //通过查glm的帮助文档来输入
summary(lofit)
输出:性别、是否有孩子、教育、是否有工作对方程的贡献不显著。说明出轨与性别、是否有孩子、教育程度、是否有工作关系不大。
Call:
glm(formula = YnAffairs ~ gender + age + yearsmarried + children +
religiousness + education + occupation + rating, family = binomial(link = "logit"),
data = Affairs)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5713 -0.7499 -0.5690 -0.2539 2.5191
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.37726 0.88776 1.551 0.120807
gendermale 0.28029 0.23909 1.172 0.241083
age -0.04426 0.01825 -2.425 0.015301 *
yearsmarried 0.09477 0.03221 2.942 0.003262 **
childrenyes 0.39767 0.29151 1.364 0.172508
religiousness -0.32472 0.08975 -3.618 0.000297 ***
education 0.02105 0.05051 0.417 0.676851
occupation 0.03092 0.07178 0.431 0.666630
rating -0.46845 0.09091 -5.153 2.56e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 675.38 on 600 degrees of freedom
Residual deviance: 609.51 on 592 degrees of freedom
AIC: 627.51
Number of Fisher Scoring iterations: 4接下来我们把这些关系不大的变量去除了,看看新模型是否拟合得更好。
lofit1 <- glm(YnAffairs ~ age+yearsmarried+religiousness+rating, data = Affairs, family = binomial(link = "logit"))
summary(lofit1)
由于lofit和lofit1是嵌套关系,所以可以使用annova函数进行比较。
对于广义线性回归,可使用卡方检验。
anova(lofit, lofit1, test = "Chisq")
输出:结果卡方检验值不显著,P值等于0.21。证明两次结果差别不大,说明只有4个预测变量的新模型和原模型拟合程度一样好。说明那些不显著的变量不会显著提高模型的预测精度。所以之后可以把这些变量去除掉。
Analysis of Deviance Table
Model 1: YnAffairs ~ gender + age + yearsmarried + children + religiousness +
education + occupation + rating
Model 2: YnAffairs ~ age + yearsmarried + religiousness + rating
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 592 609.51
2 596 615.36 -4 -5.8474 0.2108详细解释一下结果:
coef(lofit1)
输出:
(Intercept) age yearsmarried religiousness rating
1.93083017 -0.03527112 0.10062274 -0.32902386 -0.46136144
在Logistic回归中,响应变量是y=1的对数优势比。回归系数的含义是,当其他预测变量不变时,
1单位预测变量的变化,可能会引起响应变化对数优势比变化。
exp(coef(lofit1)) //由于使用了对数优势比,使用指数运算,将其计算到正常模式
输出:
(Intercept) age yearsmarried religiousness rating
6.8952321 0.9653437 1.1058594 0.7196258 0.6304248
婚龄增加一年,婚外情的优势比将乘以1.1058594。年龄增加一岁,发生婚外情的优势比将乘以0.9653437
什么是优势比?
答:优势比(odds ratio;OR)是另外一种描述概率的方式。优势比将会告诉我们某种推测的概率比其反向推测的概率大多少。换句话说,优势比是指某种推测为真的概率与某种推测为假的概率的比值。比如下雨的概率为0.25,不下雨的概率为0.75。0.25与0.75的比值可以约分为1比3。因此,我们可以说今天将会下雨的优势比为1:3(或者今天不会下雨的概率比为3:1)。
进行预测:
testdata1 <- data.frame(rating = c(1,2,3,4,5), age = c(1,1,1,1,1), yearsmarried = c(1,1,1,1,1), religiousness = c(1,1,1,1,1))
testdata1$probability <- predict(lofit1, newdata = testdata1, type = "response")
testdata1
输出:控制婚龄、宗教、年龄,改变评价,看对出轨概率的影响。
rating age yearsmarried religiousness probability
1 1 1 1 1 0.7695543
2 2 1 1 1 0.6779649
3 3 1 1 1 0.5702996
4 4 1 1 1 0.4555457
5 5 1 1 1 0.3453258# 主成分分析
主成分分析是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关(独立)变量,这些无关的变量称为主成分。主成分是对原始变量重新进行线性组合,将原先众多具有一定相关性的指标重新组合为一组新的互相独立的综合指标。
选原始数据成分的某几个代表大部分信息。
无论是主成分分析还是因子分析,都分以下7个步骤:
- 数据预处理
- 选择分析模型(主成分分析、因子分析)
- 判断要选择的主成分/因子数目
- 选择主成分/因子
- 旋转主成分/因子(可选步骤)
- 解释结果
- 计算主成分或因子得分(可选步骤)
以USJudgeRatings数据集举个例:使用 psych 包
这个数据集已经处理了缺失数据,行为观测,列记录了每一个变量的值。使用PC(主成分)分析,则第一个步骤和第二个步骤就完成了。可以先绘制碎石图,查看需要几个主成分。
fa.parallel(USJudgeRatings, fa = "pc", n.iter = 100) //绘制碎石图。输出图形后会建议你用几个主成分,看下面那一行。
pc <- principal(USJudgeRatings, nfactors = 1, rotate = "none", scores = F) //nfactor设置主成分个数。rotate指定旋转方法,scores是否计算主成分得分。
输出的PC1栏是观测变量与主成分的相关系数。h2是成分公因子方差,是主成分对每个变量的方差解释度。u2是主成分唯一性,是方差无法被主成分解释的比例。
Proportion Var则是主成分对总体方差的解释度。
再举一个相关系数的例子:
fa.parallel(Harman23.cor$cov, n.obs = 305, fa = "pc", n.iter = 100) //n.obs设置观测值。绘制碎石图,也会返回文字结果建议选择多少个主成分。
pc <- principal(Harman23.cor$cov, nfactors = 2, rotate = "none") //进行主成分分析
输出的Cumulative Proportion会显示每个主成分解释的总体占比和累计占比。
rotate参数可以设置为参数去噪。旋转方法有两种:使旋转成分保持不相关的正交旋转,使旋转成分变得相关的斜交旋转。
最流行的正交旋转是方差极大旋转,试图对载荷矩阵的列进行去噪,使得每个成分仅有一组有限的变量来解释。
# 因子分析
探索性因子分析法,是一系列用来发现一组变量的潜在结构的方法。通过寻找一组更小的、潜在的或隐藏的结构来解释已观测到的、显式的变量间的关系。本质上也是用来降维,是主成分分析的推广和发展。
适合于分析隐藏在表面现象背后的因子作用的统计模型。试图用最小个数的不可测的公共因子的线性函数与特殊因子(无法被公共因子解释的部分)之和,来描述原来的每个变量。
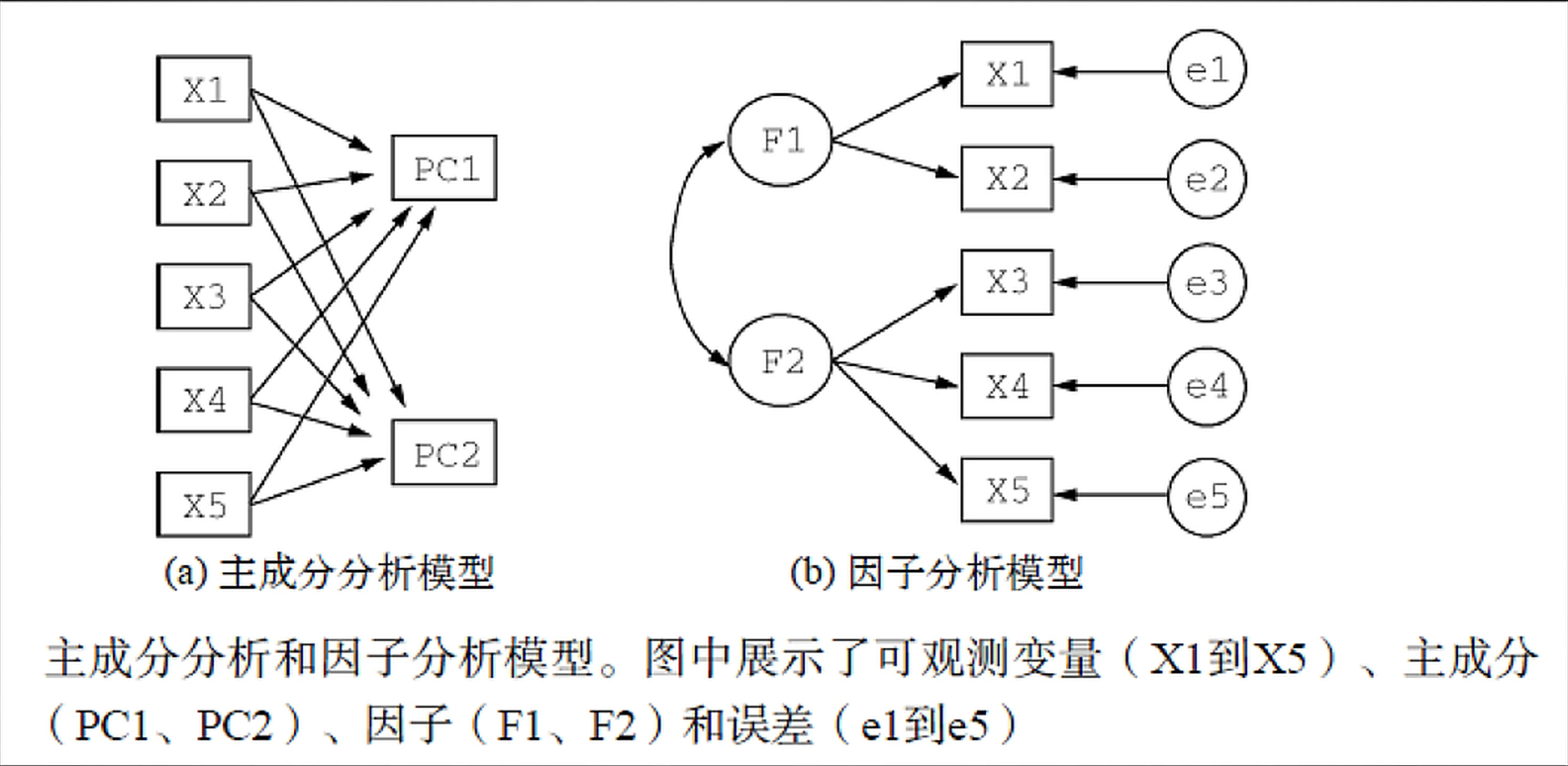
关于主成分分析和因子分析,基因学苑给了个例子。如对语文、数学、英语、历史、地理、政治、物理、化学、生物这几个变量进行分类。主成分分析得到的结果是语文、数学、英语、文科或理科。因子分析得到的是逻辑推理(数学、物理、化学、生物)、语言天赋(语文、英语)、逻辑分析(历史、政治、地理)。
因子分析是寻找的公共因子。
主成分分析和因子分析相同点:

主成分分析和因子分析不同点:

因子分析的评价结果没有主成分分析准确,计算量也比主成分分析大。但公共因子比主成分更容易被解释。
例子(步骤与主成分分析一致):
这里使用ability.cov数据集进行演示。

那么我们怎么用一组较少的潜在的心理学因素来解释参与者的测试得分呢。
options(digits = 2) //可以设置保留两位小数
covariances <- ability.cov$cov //因为原数据集是列表,所以这里单独把cov项(矩阵数据)取出来
correlations <- cov2cor(covariances) //取出来的是协方差矩阵,将covariances协方差矩阵转化为系数矩阵
fa <- fa.parallel(correlations, fa = "both", n.obs = 112, n.iter = 100) //both是既做主成分分析又做因子分析。nobs是样本数,niter是模拟分析次数。这里会输出主成分个数和因子个数以及一张碎石图。
f <- fa(correlations, nfactors = 2, rotate = "none", fm = "pa") //进行因子分析。
fm参数设定提取公共因子的方法。包括最大似然法、主轴迭代法、加权最小二乘法、广义加权最小二乘法、最小残差法。
f //直接输出f,不用summary()函数,否则结果会很少。对于以下输出结果,可以看到。因子1解释了这6个心理学测试的46%的方差,因子2解释了这6个心理学测试的14%的方差。合计起来,这两个因子就解释了这个心理学测试的60%的方差。
因子的旋转:将成分整合成更容易解释的数学方法。可以使用正交旋转和斜交旋转。
f <- fa(correlations, nfactors = 2, rotate = "varimax", fm = "pa")
输出:
Factor Analysis using method = pa
Call: fa(r = correlations, nfactors = 2, rotate = "varimax",
fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix
PA1 PA2 h2 u2 com
general 0.49 0.57 0.57 0.432 2.0
picture 0.16 0.59 0.38 0.623 1.1
blocks 0.18 0.89 0.83 0.166 1.1
maze 0.13 0.43 0.20 0.798 1.2
reading 0.93 0.20 0.91 0.089 1.1
vocab 0.80 0.23 0.69 0.313 1.2
PA1 PA2
SS loadings 1.83 1.75
Proportion Var 0.30 0.29
Cumulative Var 0.30 0.60
Proportion Explained 0.51 0.49
Cumulative Proportion 0.51 1.00
Mean item complexity = 1.3
Test of the hypothesis that 2 factors are sufficient.
The degrees of freedom for the null model are 15 and the objective function was 2.48
The degrees of freedom for the model are 4 and the objective function was 0.07
The root mean square of the residuals (RMSR) is 0.03
The df corrected root mean square of the residuals is 0.06
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy
PA1 PA2
Correlation of (regression) scores with factors 0.96 0.92
Multiple R square of scores with factors 0.91 0.85
Minimum correlation of possible factor scores 0.82 0.71可以看出,阅读和词汇在第一因子上整合较大,画图和迷宫在第二因子上整合较大。非语言智力测试在两个因子上整合较为平均。这说明存在语言智力因子和非语言智力因子。
使用正交旋转可以强制使两个因子不相关。如果想使两个因子相关,则使用斜交旋转法。
f <- fa(correlations, nfactors = 2, rotate = "Promax", fm = "pa")
注意,斜交旋转法的P是大写的。最后是输出图形的部分:
factor.plot(f, labels = rownames(f$loadings)) //第一幅图,输出斜交旋转法的结果。
fa.diagram(f, simple = F) //第二幅图,输出正交旋转法的结果。
但实际上,这两种输出图像的函数无论是对于正交、斜交还是不旋转的因子分析结果,都是可以输出的。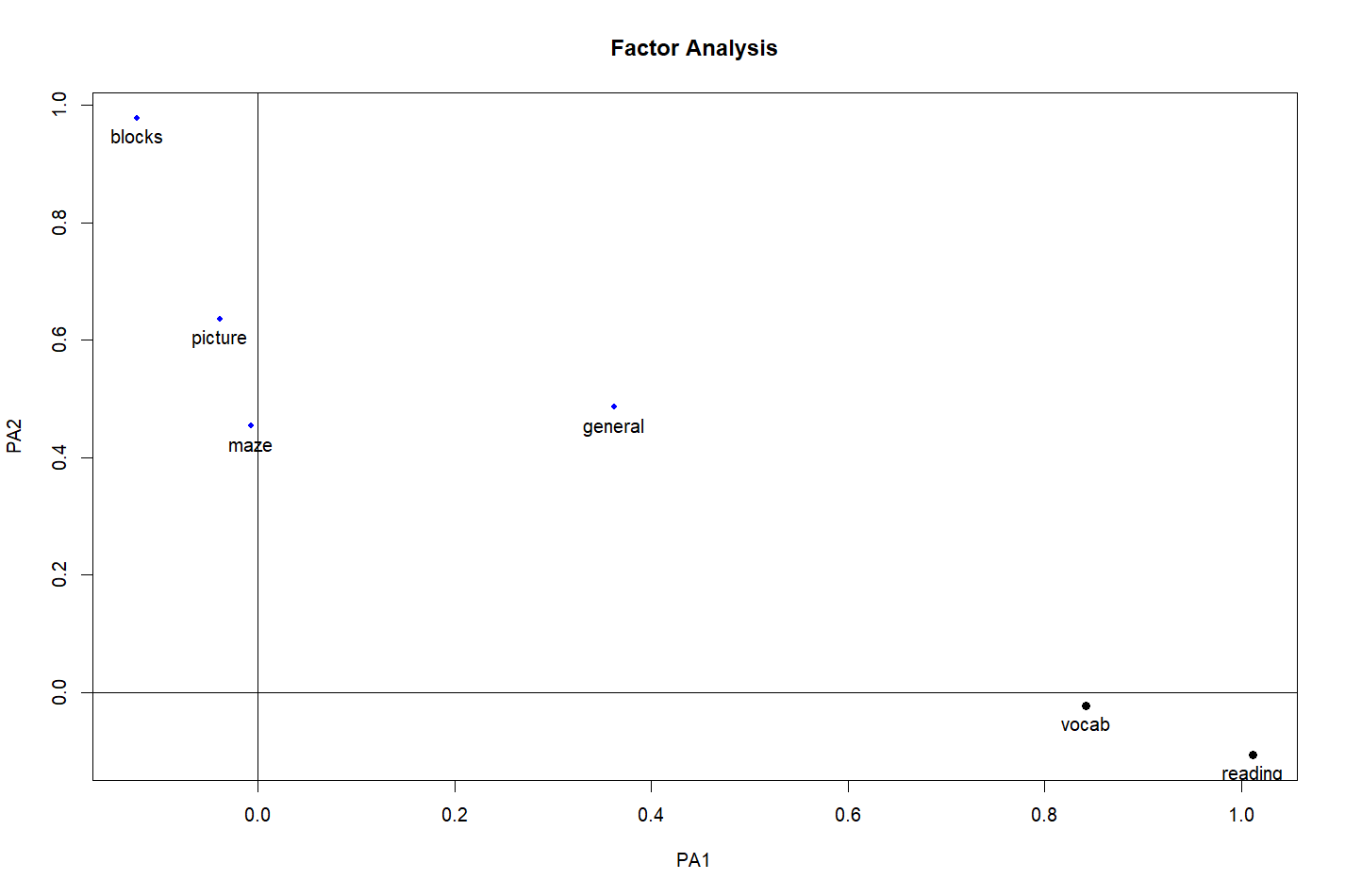
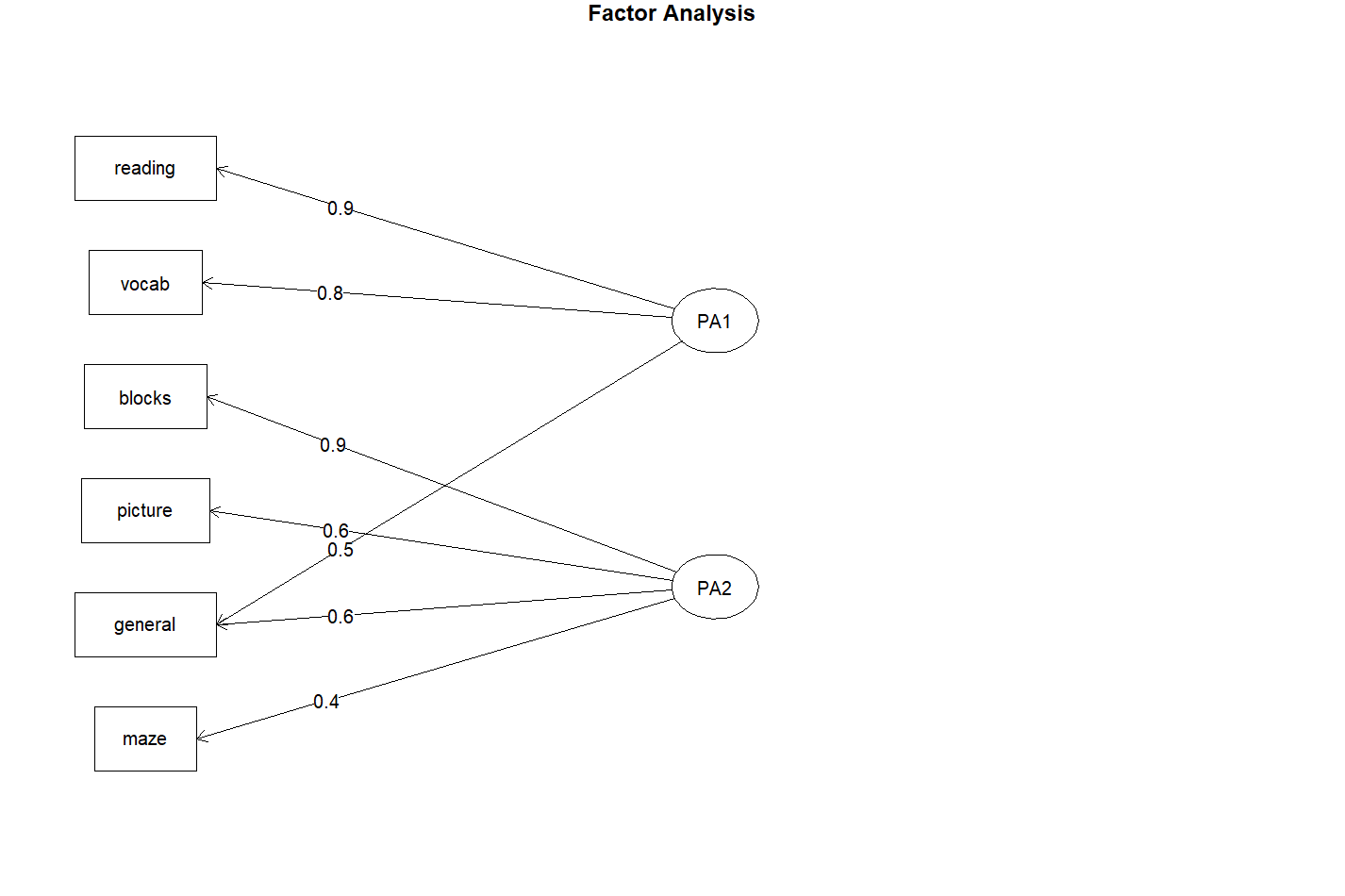
在因子分析中,加上 score 参数以获得因子得分。
f <- fa(correlations, nfactors = 2, rotate = "none", fm = "pa", score = T)
f$weights //使用这种方式查看因子得分# 购物篮分析
著名案例:啤酒和尿布。超市把啤酒和尿布放在一起提高了销量。
下面使用超市的收银单进行举例:
install.packages("arules")
library(arules)
data("Groceries")
inspect(Groceries) //这个数据比较特殊,没办法直接敲Groceries查看,需要用inspect()函数
fit <- apriori(Groceries, parameter = list(support = 0.01, confidence = 0.5)) //这里使用apriori函数进行计算。Apriori详情见下文。parameter参数中接的列表中显示,support最小支持度是0.01,confidence最小置信度是50%
inspect(fit)
输出:
lhs rhs support confidence coverage lift
[1] {curd,yogurt} => {whole milk} 0.01006609 0.5823529 0.01728521 2.279125
[2] {other vegetables,butter} => {whole milk} 0.01148958 0.5736041 0.02003050 2.244885
[3] {other vegetables,domestic eggs} => {whole milk} 0.01230300 0.5525114 0.02226741 2.162336
[4] {yogurt,whipped/sour cream} => {whole milk} 0.01087951 0.5245098 0.02074225 2.052747
[5] {other vegetables,whipped/sour cream} => {whole milk} 0.01464159 0.5070423 0.02887646 1.984385
[6] {pip fruit,other vegetables} => {whole milk} 0.01352313 0.5175097 0.02613116 2.025351
[7] {citrus fruit,root vegetables} => {other vegetables} 0.01037112 0.5862069 0.01769192 3.029608
[8] {tropical fruit,root vegetables} => {other vegetables} 0.01230300 0.5845411 0.02104728 3.020999
[9] {tropical fruit,root vegetables} => {whole milk} 0.01199797 0.5700483 0.02104728 2.230969
[10] {tropical fruit,yogurt} => {whole milk} 0.01514997 0.5173611 0.02928317 2.024770
[11] {root vegetables,yogurt} => {other vegetables} 0.01291307 0.5000000 0.02582613 2.584078
[12] {root vegetables,yogurt} => {whole milk} 0.01453991 0.5629921 0.02582613 2.203354
[13] {root vegetables,rolls/buns} => {other vegetables} 0.01220132 0.5020921 0.02430097 2.594890
[14] {root vegetables,rolls/buns} => {whole milk} 0.01270971 0.5230126 0.02430097 2.046888
[15] {other vegetables,yogurt} => {whole milk} 0.02226741 0.5128806 0.04341637 2.007235
count
[1] 99
[2] 113
[3] 121
[4] 107
[5] 144
[6] 133
[7] 102
[8] 121
[9] 118
[10] 149
[11] 127
[12] 143
[13] 120
[14] 125
[15] 219
Apriori算法是一种通过频繁项集来挖掘关联规则的算法。该算法既可以发现频繁项集,又可以挖掘物品之间关联规则。分别采用支持度和置信度来量化频繁项集和关联规则。其核心思想是通过候选集生成和情节的向下封闭检验检测两个阶段来挖掘频繁项集。
回到输出的结果:
通过购物篮分析得到了15条规则。第一条规则是,如果购物篮里有curd和yogurt,则一定有whole milk。支持度达到1%,置信度达到58.2%,lift反应相关系数,这个值越大,相关关系越大。