补充正则化、绘图以及特征映射内容。
# 序
上则贴子举的例子不含高次项特征,因此绘出的决策边界仅为一条直线,故未讲述如何绘制数据与决策边界。本贴将补充上述未涵盖的内容,并实现 logistic regression 的正则化。
# import modules
import numpy
import pandas
from matplotlib import pyplot# map feature
想要更好地拟合数据,其中一种方法是从每个数据点中创造更多特征。在 map_feature() 函数中将把特征映射到六次方多项式。 stack() 、 concatenate() 与 h/vstack() 的示例将在 Numpy学习记录 中补充。
def map_feature(X_map, degree=6):
"""
:param X_map: (ndarray Shape(m, n)) dataset, m samples by n features
:param degree: the degree of the polynomial you would like to map to
:return: a mapped dataset with more features of higher degree
"""
out = []
for i in range(1, degree+1):
for j in range(i+1):
out.append((X_map[:, 0]**(i-j) * (X_map[:, 1]**j)))
return numpy.stack(out, axis=1)# sigmoid function
后续计算损失、梯度时会经常使用该激活函数,因此不妨构造该函数以便后续调用。激活函数的公式如下:
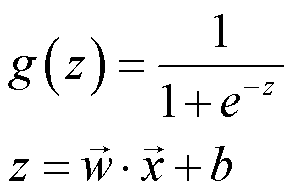
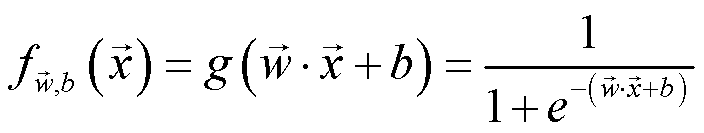
代码实现如下所示。需要注意的是,参数 z 需要传入 wx+b 。
def sigmoid(z):
return 1 / (1 + numpy.exp(-z))# compute regularized cost
在原始损失函数末尾加上正则化项便得到正则化 logistic regression 的损失计算公式:
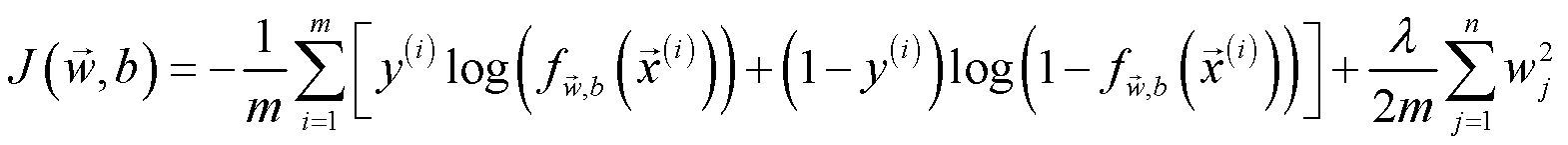
代码实现如下:
def compute_cost_reg(X, y, w_in, b_in, lambda_=0.):
"""
compute the cost over all examples
:param X: (ndarray Shape(m, n)) dataset, m samples by n features
:param y: (array_like Shape(m,)) target values for all samples
:param w_in: (array_like Shape(n,)) values of parameters of the model
:param b_in: scalar Values of bias parameter of the model
:param lambda_: the parameter of regularization
:return: the regularized loss
"""
m, n = X.shape
cost_without_reg = 0
for i in range(m):
cost_without_reg += (y[i] * numpy.log(sigmoid(numpy.dot(w_in, X[i]) + b_in)) + (1 - y[i]) * numpy.log(1 - sigmoid(numpy.dot(w_in, X[i]) + b_in)))
cost_without_reg = (-1 / m) * cost_without_reg
reg_cost = 0
for j in range(n):
reg_cost += w_in[j]**2
reg_cost = (lambda_ / (2 * m)) * reg_cost
return cost_without_reg + reg_cost# compute regularized gradient
在梯度下降过程中经历数次迭代,其中每次迭代需重新计算梯度。不妨构造一枚计算梯度的函数以便调用并简化梯度下降的代码。
其中,计算正则化梯度的数学公式如下:
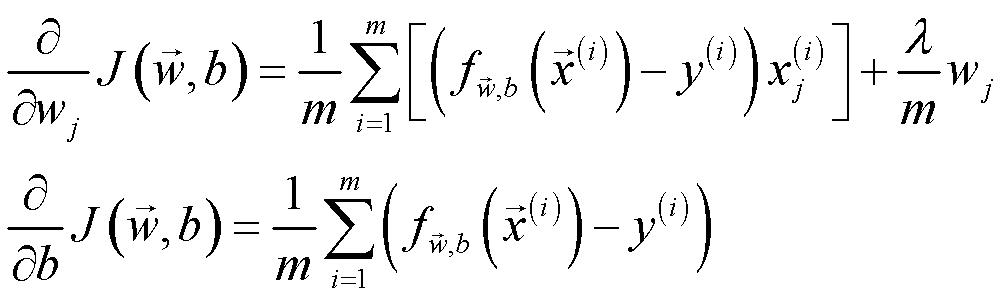
代码实现如下:
def compute_gradient(X, y, w_in, b_in, lambda_=0):
"""
compute gradient for each iteration
:param X: (ndarray Shape(m, n)) dataset, m samples by n features
:param y: (array_like Shape(m,)) target values for all samples
:param w_in: (array_like Shape(n,)) values of parameters of the model
:param b_in: scalar Values of bias parameter of the model
:param lambda_: the parameter of regularization
:return: the gradient dj_dw and dj_db
"""
m, n = X.shape
dj_dw = numpy.zeros(n)
dj_db = 0
# 计算w的梯度
for j in range(n):
for i in range(m):
dj_dw[j] += (sigmoid(numpy.dot(w_in, X[i]) + b_in) - y[i]) * X[i][j]
dj_dw /= m
# 为每一个特征的梯度末尾添加正则化项的偏导数
for j in range(n):
dj_dw[j] += (lambda_ / m) * w_in[j]
# 计算截距项的梯度
for i in range(m):
dj_db += (sigmoid(numpy.dot(w_in, X[i]) + b_in) - y[i])
dj_db /= m
return dj_dw, dj_db# gradient descent
传入映射后的数据集、模型初始参数、学习率、迭代次数及正则化系数并调用正则化损失计算函数、激活函数与正则化梯度计算函数进行梯度下降,最后返回学习得到的模型参数及最后的损失。其中,梯度下降同步更新数学公式如下,较非正则化回归多了正则化项:
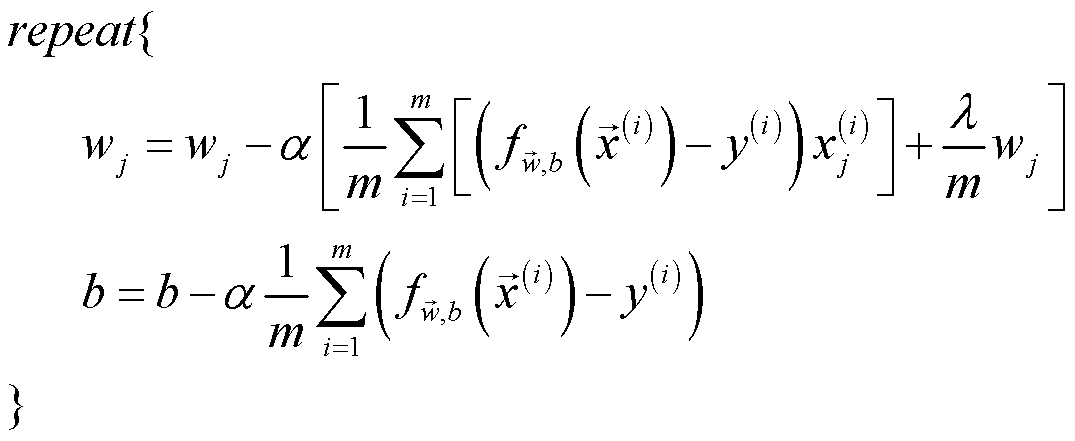
代码实现如下:
def gradient_descent(X, y, w_in, b_in, alpha, iters, lambda_=0):
"""
run gradient descent
:param X: (ndarray Shape(m, n)) dataset, m samples by n features
:param y: (array_like Shape(m,)) target values for all samples
:param w_in: (array_like Shape(n,)) values of parameters of the model
:param b_in: scalar value of bias parameter of the model
:param alpha: learning rate α
:param iters: iterations for gradient descent
:param lambda_: the parameter of regularization
:return:
"""
m_in, n_in = X.shape
for inum in range(iters):
dj_dw, dj_db = compute_regularized_gradient(X, y, w_in, b_in, lambda_)
for j in range(n_in):
w_in[j] = w_in[j] - alpha * dj_dw[j]
b_in = b_in - alpha * dj_db
loss_in = compute_regularized_cost(X, y, w_in, b_in, lambda_)
return w_in, b_in, loss_in# predict
正则化仅作用于学习模型参数,将映射后的数据集与学习得到的参数传入激活函数中,将激活函数输出结果按如下规则进行分类,得到预测的目标变量。
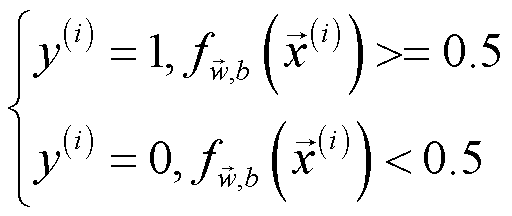
实现代码如下:
def predict(X_pred, w_pred, b_pred):
"""
make predictions with learned w and b
:param X_pred: data set with m samples and n features
:param w_pred: values of parameters of the model
:param b_pred: scalar value of bias parameter of the model
:return:
"""
predictions = sigmoid(numpy.dot(X_pred, w_pred) + b_pred)
p = [1 if item >= 0.5 else 0 for item in predictions]
return numpy.array(p)# plot data
将正例、负例数据展示到坐标轴上,并以不同符号颜色进行区分。在此运用Boolean list筛选数组内的元素,需要注意的是被筛选数组的维度。数组的筛选方法具体见贴子 Numpy学习记录 。
def plot_data(X_train, y, ax, positive_label='y=1', negative_label='y=0'):
# 正例列表,当y=1时为True,否则为False。
# 需要注意的是shape为(m,1),用它过滤shape不为(m,1)或(m,)的ndarray时会匹配不上。
# 而这里X_train为(100,2),因此需要将Boolean list通过.reshape(-1)转为(m,)
positive = y == 1
# 负例列表,当y=0时为True,否则为False。需要注意的是shape为(m,1)
negative = y == 0
# 通过上述Boolean list绘制正例。用pyplot.scatter()也行
ax.plot(X_train[positive.reshape(-1), 0], X_train[positive.reshape(-1), 1], 'k+', label=positive_label)
# 通过上述Boolean list绘制负例
ax.plot(X_train[negative.reshape(-1), 0], X_train[negative.reshape(-1), 1], 'yo', label=negative_label)# plot decision boundary
在此使用 pyplot.contour() 绘制决策边界,函数 meshgrid() 常与等高线函数一同出现,后者旨在生成网格点,为属性值提供坐标。
meshgrid() 的作用如下图所示:
接下来简单介绍 pyplot.contour() ,前两个参数 X=, Y= 决定位置,既可以传X=XX, Y=YY也可以传X=x, Y=y。第三个参数 Z= 决定位置上的值,需要传维度为 (len(y), len(x)) 的属性值数组。 levels= 传入一个包含想要显示为等高线的值的列表,比如这里决策边界的值为0.5,那么可以传入[0.5]。
def plot_decision_boundary(w_db, b_db, ax):
# 画等高线
x1_ax_contour = numpy.linspace(-1, 1.5, 100)
x2_ax_contour = numpy.linspace(-1, 1.5, 100)
values_contour = numpy.zeros((len(x1_ax_contour), len(x2_ax_contour)))
for i in range(len(x1_ax_contour)):
for j in range(len(x2_ax_contour)):
values_contour[i][j] = sigmoid(numpy.dot(map_feature(numpy.array([x1_ax_contour[i], x2_ax_contour[j]]).reshape((1, 2))), w_db) + b_db)
ax.contour([x1_ax_contour, x2_ax_contour], values_contour.T, levels=[0.5], colors='red')最后讲一下values_contour为什么要转置。由于等高线函数传入决定位置的参数为两个一维列表,第一个参数决定X轴上的位置,第二个参数决定Y轴上的位置。若第一个参数的维度为(n,),第二个参数的维度为(m,),那么等高线函数认为的网格点如下:

网格点维度为(m, n),而通过两个循环计算得到的属性值数组的维度为(n, m)。因此需要将后者转置,才能使每一个网格点对应一个正确的属性值。此外, numpy.meshgrid() 函数返回的每一个矩阵仅对应一个坐标轴上的位置。当把返回的所有矩阵组合在一起,每一个表示一个坐标轴上的位置时,才能形成该多维坐标系上确切的点坐标。
# main
从txt文件中导入数据并对数据集特征映射。初始化所有模型参数后,将它们与学习率、迭代次数、正则化系数一同传入梯度下降函数。值得一提的是,正则化回归的梯度下降函数与非正则化的别无二致,区别仅存在于正则化损失计算与正则化梯度计算。
# 导入数据到一个DataFrame
data = pandas.read_csv('data/data_regular.txt', header=None)
# 获取列数(包括输出变量)
colNum = data.shape[1]
# 定义数据集(不含输出变量)
X_train = data.iloc[:, :colNum - 1]
X_train = numpy.array(X_train.values)
# 特征映射
X_mapped = map_feature(X_train)
# 定义输出空间
y_train = data.iloc[:, colNum - 1: colNum]
y_train = numpy.array(y_train.values)
# 获取样本量和特征数
m, n = X_mapped.shape
# 初始化w, b
numpy.random.seed(1)
w_init = numpy.random.rand(X_mapped.shape[1]) - 0.5
b_init = 1.
# 正则化梯度下降求解模型参数
w, b, loss = gradient_descent(X_mapped, y_train, w_init, b_init, alpha=0.01, iters=10000, lambda_=0.01)
print(f'w = {w}\nb = {b}\nloss = {loss}')
# 根据学习得到的参数进行目标变量的预测
pred = predict(X_mapped, w, b)
# 将预测的目标变量与真实目标变量相比,得到准确率
accuracy = numpy.mean(pred == y_train.reshape(-1)) * 100
print(f'Train Accuracy: {accuracy}')
# 初始化figure和axis
fig, ax = pyplot.subplots()
# 展示数据
plot_data(X_train=X_train, y=y_train, ax=ax)
# 绘决策边界
plot_decision_boundary(w, b, ax)
pyplot.show()# 补充
数组的堆并和连接将在 Numpy学习记录 一贴中展示。
完整代码