regularized_multiple_linear_regression

来点正则化震撼。

# 序

之前把截距项 b 一同创建到参数向量 w 中了，今后的实例将把它们分开。

# import modules

仅导入 numpy 与 pandas 分别进行数学运算与数据导入。

import numpy
import pandas

# compute regularized cost

定义代价计算函数有助于计算每一次迭代的代价结果，之后可以用来作图和代价输出。此处代价函数考虑了正则化项，如下图所示。

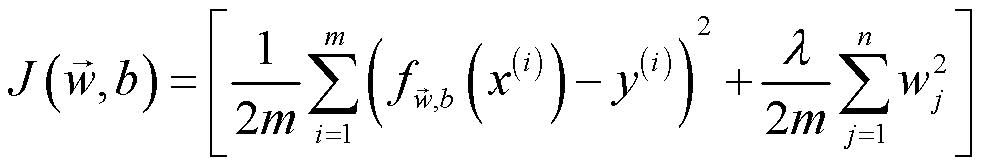
def compute_cost_function(X, y, w, b, lambda_):
    # 样本量
    m = X.shape[0]
    # 特征数量
    n = X.shape[1]
    # 初始化平方误差项与正则化项
    squared_error = 0
    regularization_term = 0
    # 计算平方误差项
    for i in range(m):
        squared_error += (numpy.dot(w, X[i]) + b - y[i])**2
    squared_error /= 2 * m
    # 计算正则化项
    for j in range(n):
        regularization_term += w[j]**2
    regularization_term = regularization_term * lambda_ / (2 * m)
    return squared_error + regularization_term

# compute gradient

完成 regularized_logistic_regression 后意识到功能应尽可能清晰，因此将计算梯度功能单独写为一个函数。

计算梯度的数学公式为：

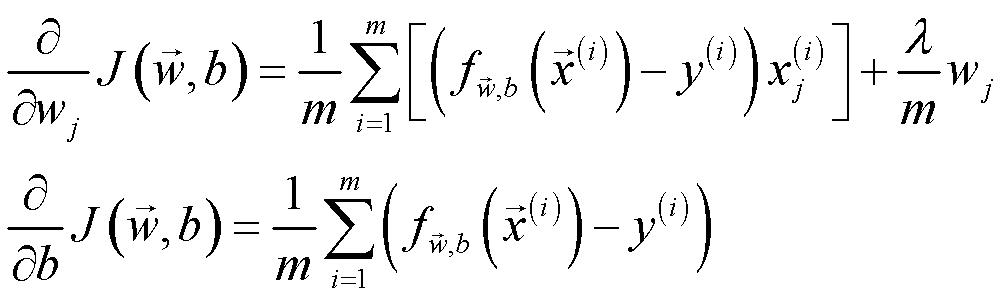
实现代码如下：

def compute_gradient(X_in, y_in, w_in, b_in, lambda_):
    # m为样本量，n为特征数量
    m, n = X_in.shape
    # 初始化dj_dw列表与dj_db
    dj_dw = numpy.zeros(n)
    dj_db = 0
    # 计算dj_dw
    for j in range(n):
        for i in range(m):
            dj_dw[j] += (numpy.dot(X_in[i], w_in) + b_in - y_in[i]) * X_in[i][j]
        dj_dw[j] /= m
        # 加上正则化项
        dj_dw[j] += (lambda_ / m) * w_in[j]
    # 计算dj_db
    for i in range(m):
        dj_db += numpy.dot(X_in[i], w_in) + b_in - y_in[i]
    dj_db /= m
    return dj_dw, dj_db

# regularized gradient descent

公式如下图所示，图中的中括号内便是上面函数计算的梯度。

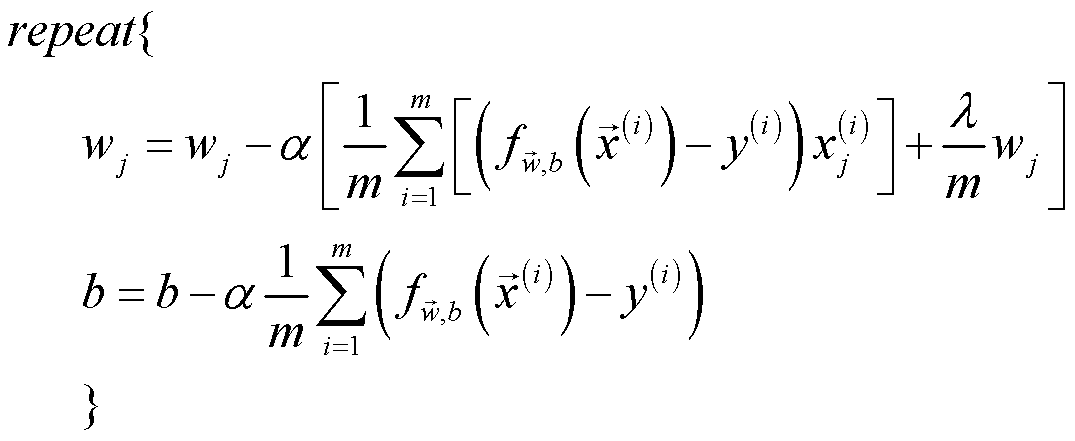
def gradient_descent(X_in, y_in, w_in, b_in, iters, alpha, lambda_):
    # m为样本数量，n为特征数量
    m, n = X_in.shape
    for i in range(iters):
        dj_dw, dj_db = compute_gradient(X_in, y_in, w_in, b_in, lambda_)
        for j in range(n):
            w_in[j] = w_in[j] - alpha * dj_dw[j]
        b_in = b_in - alpha * dj_db
    loss = compute_cost_function(X_in, y_in, w_in, b_in, lambda_)
    return w_in, b_in, loss

# main function

主函数里进行数据导入，并切割为训练样本的自变量数组与目标变量数组。

# 导入数据
data = pandas.read_csv('ex1data2.txt', header=None, names=['Size', 'Bedrooms', 'Price'])
# Mean Normalization，也可以将.loc()替换为.iloc()后列明替换为索引
for col in ['Size', 'Bedrooms']:
    data.loc[:, col] = (data.loc[:, col] - data.loc[:, col].mean()) / (data.loc[:, col].max() - data.loc[:, col].min())
data.loc[:, 'Price'] = data.loc[:, 'Price'].apply(lambda x: x / 10000)
# 定义训练样本的自变量2D array X_train与目标变量1d array y_train
X_train = data.iloc[:, 0:data.shape[1] - 1]  # 获得的是DataFrame
X_train = numpy.array(X_train.values)  # 这样获得一个2D array，如果转成matrix后面X_train[i]就会是一个2D array，不方便操作。
# X_train = numpy.matrix(X_train.values)
# numpy.array(X_train[i].flatten())
y_train = numpy.array(data.iloc[:, data.shape[1] - 1:data.shape[1]].values)
# 初始化w和b，w是一个1d array
w = numpy.zeros(X_train.shape[1])
b = 0.
# 输入λ、α与迭代次数
lambda_ = float(input('Lambda:'))
alpha = float(input('alpha:'))
iters_ = int(input('iters:'))
# 进行正则化线性回归梯度下降求解
w, b, tt_cost = gradient_descent(X_train, y_train, w, b, iters_, alpha, lambda_)
# 输出结果
print(f'w:{w}\nb:{b}\ntotal_cost:{tt_cost}')

# 补充

将导入的数据切割成训练样本自变量 X_train 的时候一定注意把它转换成 2d array ，而不是 matrix 。

当 λ 设为0时将与普通多元线性回归无异。

完整代码

GitHub